"... local concentration factors should be considered when choosing the location of devices that protrude into the stream from aircraft fuselages or missiles, or when determining anti-icing heat requirements for the protection of these devices."

From NACA-TN-3410.

NACA-TN-3153, "Variation of Local Liquid-Water Concentration about an Ellipsoid of Fineness Ratio 5 Moving in a Droplet Field" ¹

and

NACA-TN-3410, "Variation of Local Liquid-Water Concentration about an Ellipsoid of Fineness Ratio 10 Moving in a Droplet Field" ²

Summary

The concentration of water-drops varies with distance from a surface in flight.

Abstract

Trajectories of water droplets about an ellipsoid of revolution with a fineness ratio of 5 (which often approximates the shape of an aircraft fuselage or missile) were computed with the aid of a differential analyzer. Analyses of these trajectories indicate that the local concentration of liquid water at various points about an ellipsoid varies considerably and under some conditions may be several times the free-stream concentration. Curves of the local concentration factor as a function of spatial position were obtained and are presented in terms of dimensionless parameters Reo (free-stream Reynolds number) and K (inertia), which contain flight and atmospheric conditions. These curves show that the local concentration factor at any point is very sensitive to change in the dimensionless parameters Reo and K. These data indicate that the expected local concentration factors should be considered when choosing the location of, or when determining anti-icing heat requirements for, water- or ice-sensitive devices that protrude into the stream from an aircraft fuselage or missile. Similarly, the concentration factor should be considered when choosing the location on an aircraft of instruments that measure liquid-water content or droplet-size distribution in the atmosphere.

Discussion

NACA-TN-3135 details an ellipsoid of fineness ratio 5, and NACA-TN-3410 details an ellipsoid of fineness ratio 10, and includes comparisons with the other ellipsoid.

These have many similarities to the analyses in Bodies of Revolution, so readers may wish to review that before proceeding here.

NACA-TN-1424 mentioned that the results from multicylinder instruments might be affected by the airplane body deflecting water-drop trajectories, and giving distorted values along the length of the instrument protruding out from the airplane body. NACA-TN-3153 and NACA-TN-3410 give a way of assessing water drop concentrations off of the airplane body.

Most of the discussion and figures will be from NACA-TN-3153, except as noted.

INTRODUCTION
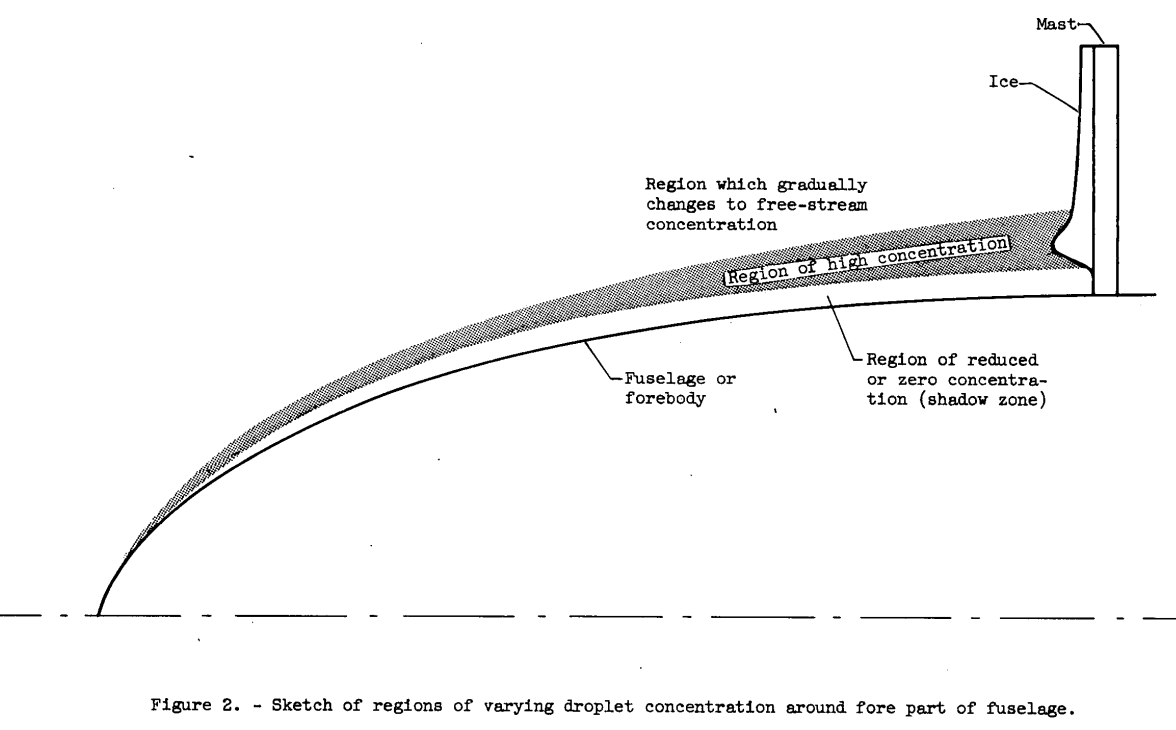
It is generally recognized that an aircraft moving through a cloud alters the concentration of cloud droplets in the immediate vicinity of the aircraft. For example, the peculiar distributions of ice often found on aircraft antenna support arms or on pitot static tubes after flight through supercooled clouds are indications that the concentration of liquid water in the vicinity of the fuselage is considerably altered by the air flow about the fuselage. This effect is illustrated by the photographs of figure 1, which show ice formed on instrument support rods mounted on the side and bottom of the fuselage of a B-25 aircraft during flight through a supercooled cloud. As indicated by the ice formations of figure 1, there is frequently a region of reduced (or zero) droplet concentration next to the aircraft surface, followed by a narrow region of greatly increased droplet concentration farther out. Beyond the narrow region of high concentration, the droplet concentration gradually decreases toward the free-stream value with increase in distance from the surface of the aircraft.

[We saw the icing rate meter in the review NACA-RM-A9C09 instruments.]

Note also the ice on the leading edge of the aircraft nose.

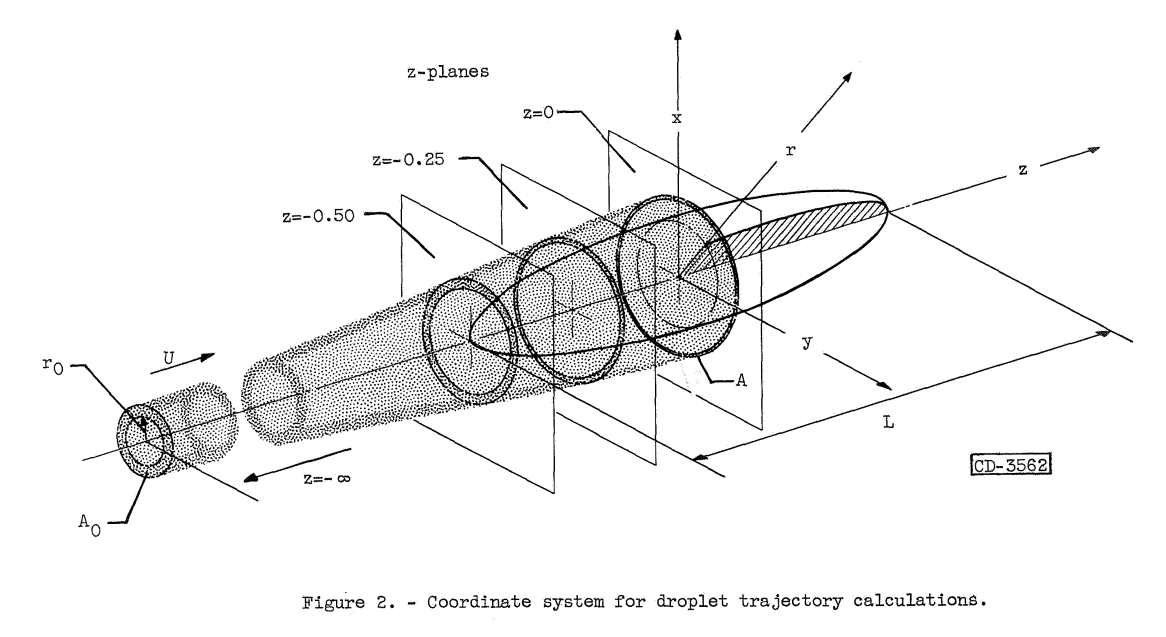
An analysis coordinate system and methods similar to Bodies of Revolution were used.

Shadow Zone
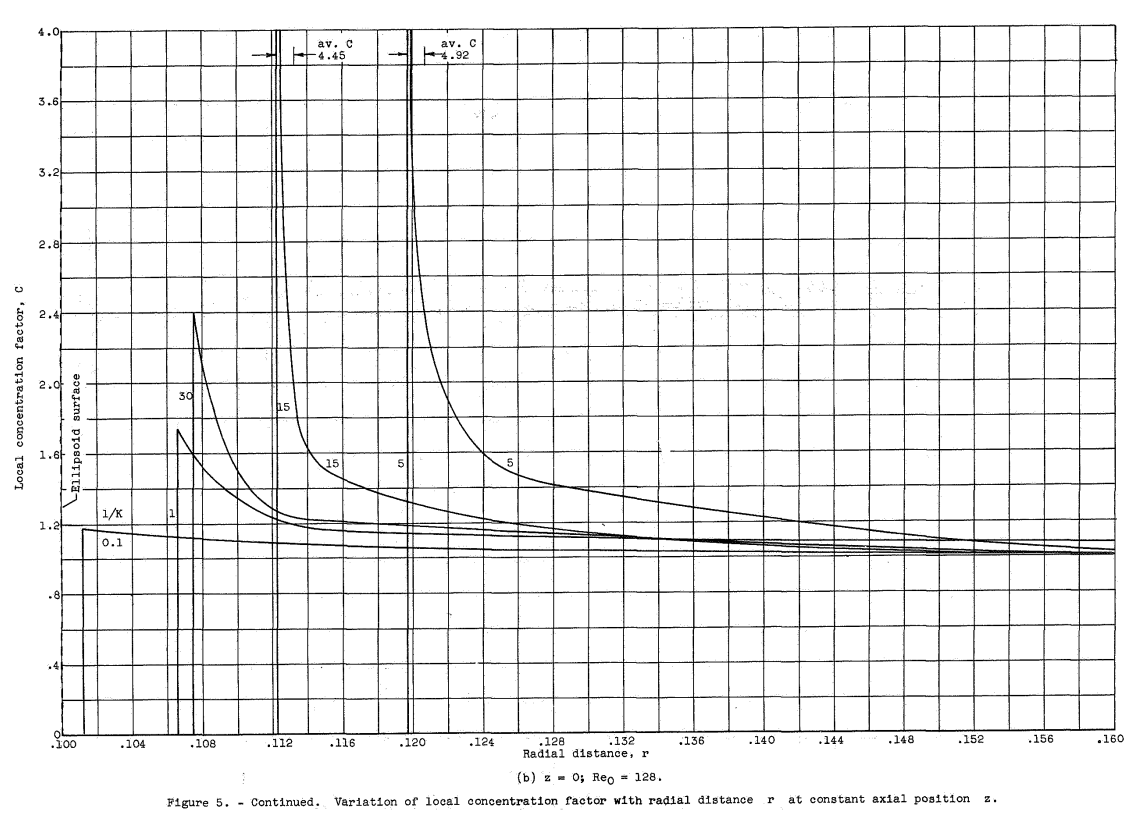
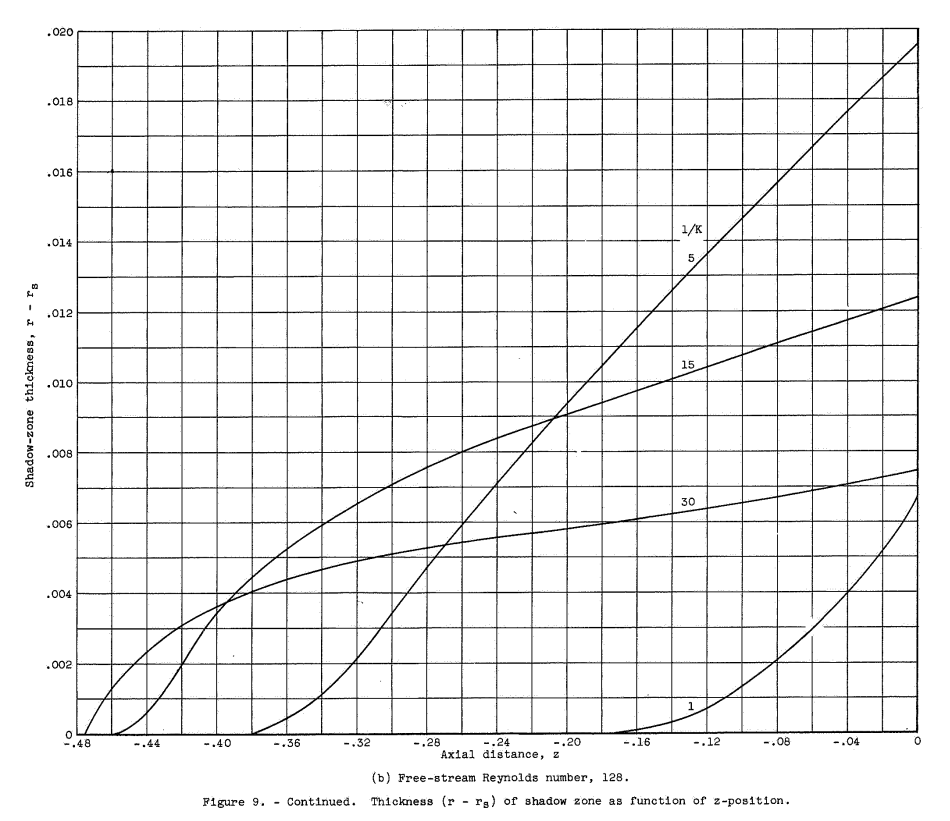
The region of zero concentration adjacent to the surface of the ellipsoid, which is evident in figure 5, will be called the shadow zone. This region is protected from droplet penetration by the air-flow characteristics ahead of and in the vicinity of the forward positions of the ellipsoid. The thickness (r - rs) of the shadow zone at each z position of the body for various Reo and K values is given in figure 9. Generally, the thickness of the shadow zone increases as z approaches 0. The shadow-zone thickness is 0 at the nose for all values of Reo and K shown in figure 9 and becomes of finite thickness at a z position that depends on Reo and K.

Comparison of ellipsoid results

From NACA-TN-3410:

With the use of the same flight and atmospheric conditions, a comparison with the 20-percent-thick ellipsoid is possible, as shown in figure 11. The abscissa is the distance from the ellipsoid surface, in inches, at z = 0. For both the 10- and 20-percent-thick ellipsoids, the major axis length is 20 feet, the flight speed is 300 miles per hour, the altitude is 15,000 feet, and the volume-median droplet diameter is 20 microns. For both bodies the peak value of the concentration factor considerably decreases as the distribution broadens from uniform droplets to a [Langmuir] "C" distribution (defined in ref. 1). Also, the region that was a former shadow zone with zero concentration for the cloud condition with uniform droplets becomes an area with a small concentration factor. A comparison of concentration-factor curves calculated for droplet-size distributions estimated to be present in clouds, such as shown in figure 11, shows good qualitative agreement with the shape of actual ice formations obtained on rod-shaped objects in flight through the clouds (fig. 1).

From NACA-TN-3410.

However, note that K is based on ellipsoid length, not diameter, so for the same diameter at the same conditions the K values will differ by a factor of 2 for the different ellipsoids. If the same body diameter were used, resulting in different body lengths, then a figure like Figure 11 would have more similar shadow zone thicknesses.

Effect on multicylinder measurements

Fortunately, most liquid-water-content data taken with rotating of multicylinders are not too much in error from these factors, because the cylinders are, in practice, generally located far enough from the fuselage so that approximately free-stream conditions prevail. Therefore, the average concentration factor at the position of measurement gives a fair indication of the degree of error in measuring liquid-water content In typical installations (ref. 11), the lowest cylinder is about 16 inches from the aircraft surface and the top cylinder is about 34 inches from the surface. With the assumed 100-foot ellipsoid moving at 300 mph at 15,000 feet with an air temperature of 10 F and a "C" distribution with a 20-micron volume-median droplet diameter, the variation of concentration factor is given in figure 10(d). At 16 inches from the surface C = 1.095 (about 10 percent high), and at 34 incr C = 1.04 (about 4 percent high). Thus the liquid-water-content measurements would be less than 10 percent too high. Actually, the values of liquid-water content summarized in references 14 and 15 may have a somewhat smaller error due to this effect than indicated by this example, because many of the measurements were obtained by using the local airspeed rather than the free-stream velocity for calculating the total catch of each cylinder. However, in spite of the relatively good location of rotating multicylinders, observers have reported occasional cases where the lower cylinder cause it excessively large or small amounts of ice. This was particularly true if the aircraft had a tendency to yaw during the measurements and thus alter the position of the shadow and peak-concentration zones.

Reference 11 is NACA-RM-E53D23, Procedure for Measuring Liquid-Water Content and Droplet Sizes in Super-cooled Clouds by Rotating Multicylinder Method".

Conclusions

NACA-TN-3153:

CONCLUDING REMARKS
The data of this report are applicable in a quantitative manner only to ellipsoids of revolution with a fineness ratio of 5. They also apply approximately in the vicinity of the nose section of a body of revolution that can be physically matched with the nose section of a fineness-ratio 5 ellipsoid of a given length. Because many bodies of revolution of interest are different in shape from an ellipsoid, the data of this report are primarily useful in pointing out in a qualitative manner the type of variation in liquid-water concentration that might be expected in the vicinity of a body of revolution in flight through a droplet field. The analysis indicates that, for some combinations of the dimensionless parameters Reo and K, the value of the local concentration of liquid water may vary from O to several times the free-stream value, depending on the location of the point being considered. Further, the calculations show that the magnitude of the concentration factor at any point is very sensitive to change in the parameters Re and K.

NACA-TN-3410:

CONCLUDING REMARKS The significance of the spatial variation of liquid-water content and droplet size is discussed thoroughly in reference 1. The effect of the spatial variation on measuring instruments and on the rotating multicylinder method is also evaluated in reference 1. The importance of avoiding measurements of liquid water and droplet size in the region of variation of droplet concentration in the vicinity of an aircraft fuselage is emphasized, because the correction of the indicated water content and droplet-size distributions to free-stream conditions would be very involved.
The data of this report are applicable in a quantitative manner only to ellipsoids of revolution with a fineness ratio of 10. As was stated in reference 1 for a thicker body (fineness ratio of 5), these data also apply approximately in the vicinity of the nose section of a body of revolution that can be physically matched with the nose section of a 10-percent-thick ellipsoid of a given length. The data are particularly applicable if the afterbody does not appreciably alter the air-flow field ahead of the ellipsoid section from that attendant to an ellipsoid. Because many bodies of revolution of interest are different in shape from an ellipsoid, the data of this report and reference 1 are primarily useful in pointing out in a qualitative manner the type of variation in liquid-water concentration that might be expected In the vicinity of a body of revolution In flight through a droplet field.

NACA-TN-3153 and NACA-TN-3410 give a way of assessing water drop concentrations off of the airplane body.

However, despite the many detailed data charts (the publications are 69 and 52 pages each), one will often find that a condition of interest is not close to a case detailed in the publications. The relationships can be highly non-linear, and interpolation is challenging. In the current times, there are ample 2D and 3D water-drop trajectory tools to make an assessment.

Figures 10d and 11 above shows a rather smooth result when using a drop size distribution. I suspect that engineering judgement and/or artistic license was used to produce the curves. In practice, when using a seven bin Langmuir distributions, one is likely to see seven spikes, one for each drop size, albeit with attenuated peaks. Fine resolution is required to resolve the spikes. The spikes are an artifact of the discrete approximation analysis used. The ice shapes in Figure 1 show what a continuous, natural distribution produces.

Related

For a study on the effect of shadow zones on instrument locations, see:
- Cook, Donald: Unusual natural icing encounters during Boeing 777 flight tests. 35th Aerospace Sciences Meeting and Exhibit. AIAA-97-0304. 1997. arc.aiaa.org

For a more recent 3D study on shadow zones, see:
- Jackson, Darren, et al.: Certification and integration aspects of a primary ice detection system. 39th Aerospace Sciences Meeting and Exhibit. AIAA-2001-0398. 2001. arc.aiaa.org

Citations

From scholar.google.com:

NACA-TN-3153: 9 citations
NACA-TN-3410: 4 citations

Related

This is part of the Water Drop Impingement on Surfaces thread.

Notes