Bodies of Revolution

"The presence of radomes and instruments that are sensitive to water films or ice formations in the nose section of all-weather aircraft and missiles necessitates a knowledge of the droplet impingement characteristics of bodies of revolution."

1

Figure 1. Coordinate system for droplet trajectory calculations about an ellipsoid of revolution of fineness ration 5.

Summary

Water-drop impingement on several bodies of revolution is quantified.

Discussion

NACA-TN-4092 4 notes:

The impingement characteristics of bodies of revolution are of interest because such bodies are representative of many aircraft components subject to icing such as radomes, body noses, engine accessory housings, and the large spinners of turboprop engines.

NACA-TN-3099 1 is the first in a series and has a rather complete description of the analysis methods, so the discussion below refers to that, unless noted otherwise.

Flow field

Potential flow can be determined in 2D radial coordinates as well as 2D Cartesian coordinates. This was used to assess several geometries.

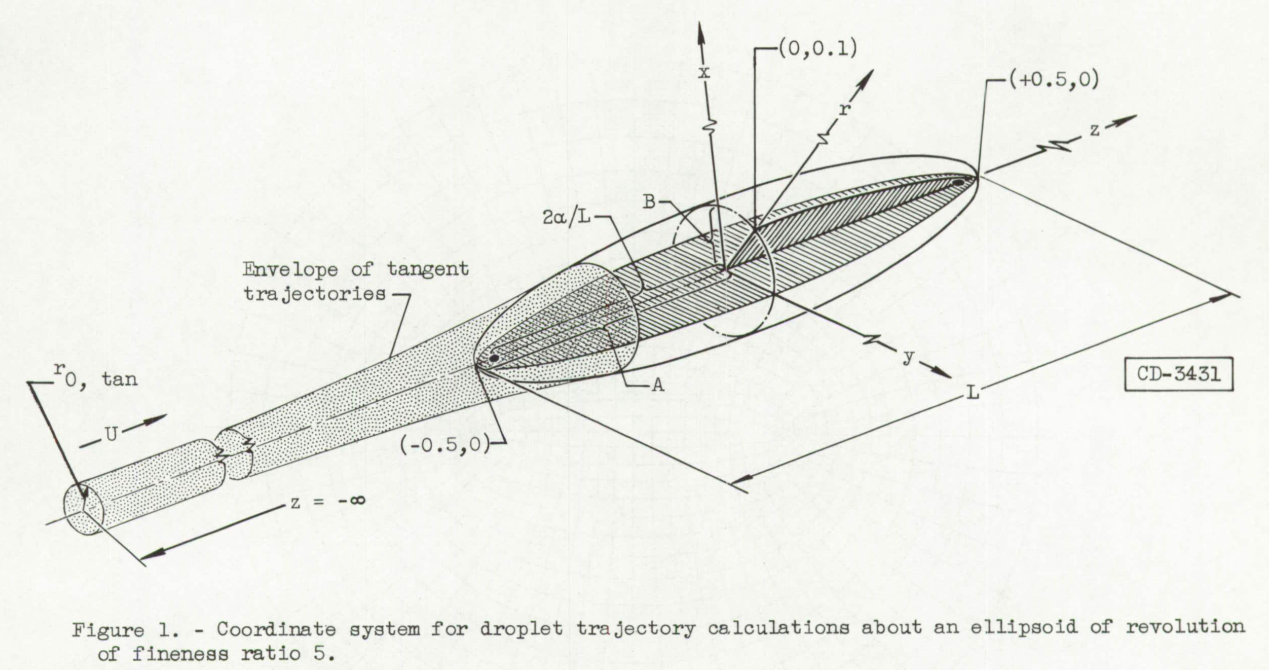
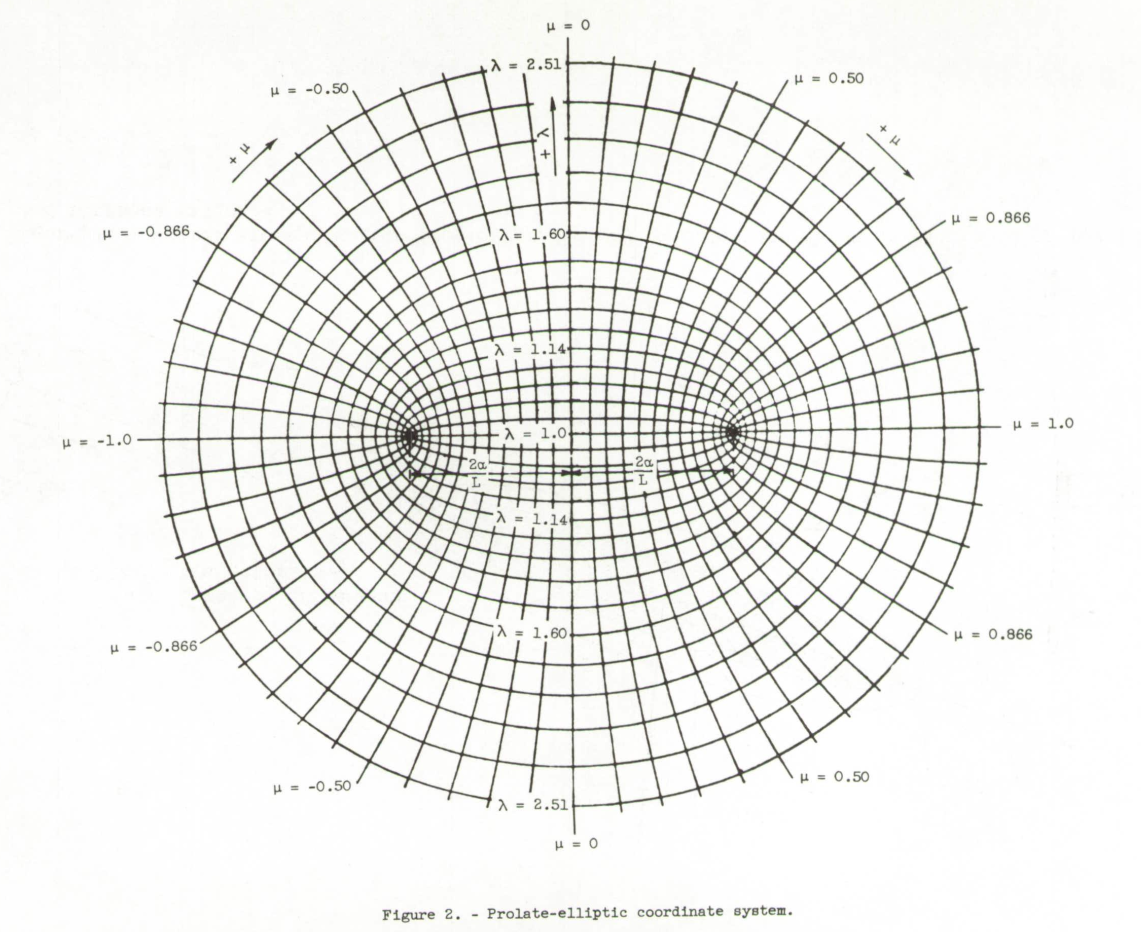
The air velocity components for incompressible nonviscous flow about a prolate ellipsoid of revolution are obtained from the exact solution of Laplace's equation In prolate-elliptic coordinates (fig. 2) given by Lamb (ref. 3).

Figure 2. Prolate Elliptic Coodinate System.

Impingement

Water-drop trajectories could then be calculated. Results were presented in several forms. Dimensionless parameters similar to the in Mathematical Investigation of Water Droplet Trajectories were used to concisely summarize a wide range of results.

Figure 4.png

Figure 6.png

While results were presented over a wide range of conditions, for some cases the range may not be enough.

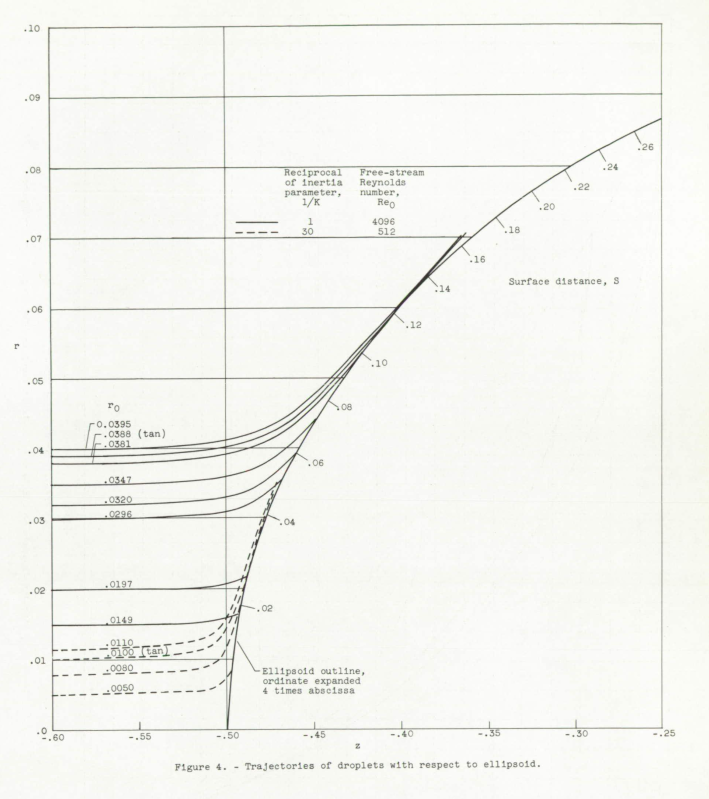
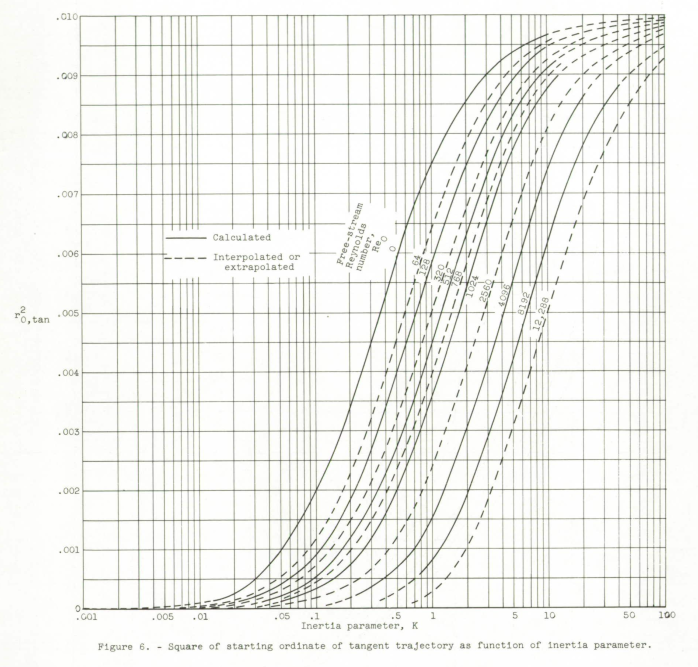
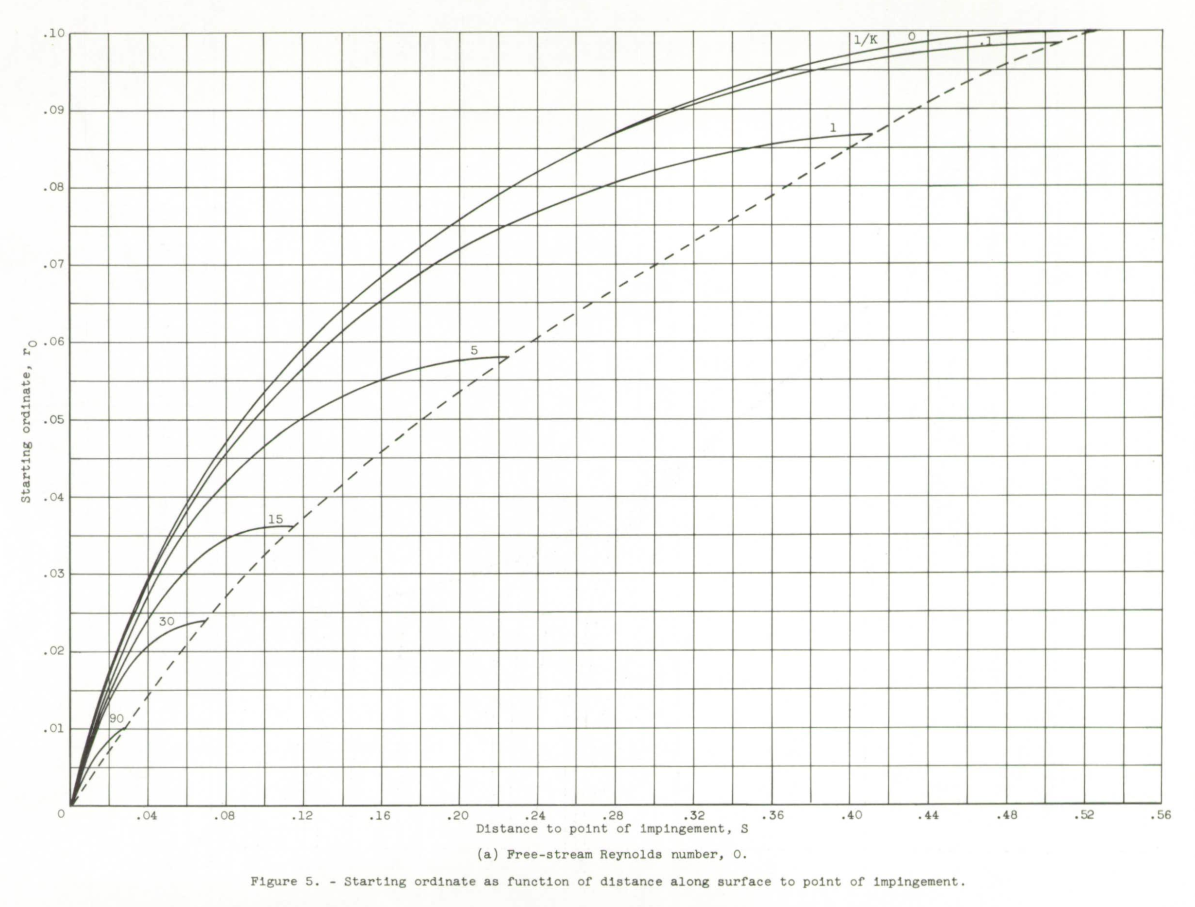
The scale factors used in the differential analyzer to solve the equations for the range of conditions presented in figures 5 to 10 and the near-parallelism of the trajectories to the surface at large values of 1/K made it impossible to obtain sufficient accuracy to present detailed data, such as the rate of local impingement of water, at points along the surface of the ellipsoid, for values of 1/K > 90 for Re_0 = 0 and 1/K > 30 for Re_0 > 128. From Table I, it can be seen that, for bodies as large as the fuselage of cargo or passenger airplanes, these conditions are not uncommon. Examination of figures 5 and 10 shows, however, that the extent (usually Sm < 0.03) and rate of local impingement are small in this Re_0 and K region. Therefore, in this region a knowledge of the extent of the impingement zone and the total rate of impingement of water as calculated from the data of figures 8 and 6, respectively, is sufficient for most applications.

Figure 5. Starting point ordinate as function of distance along surface to point of impingement.

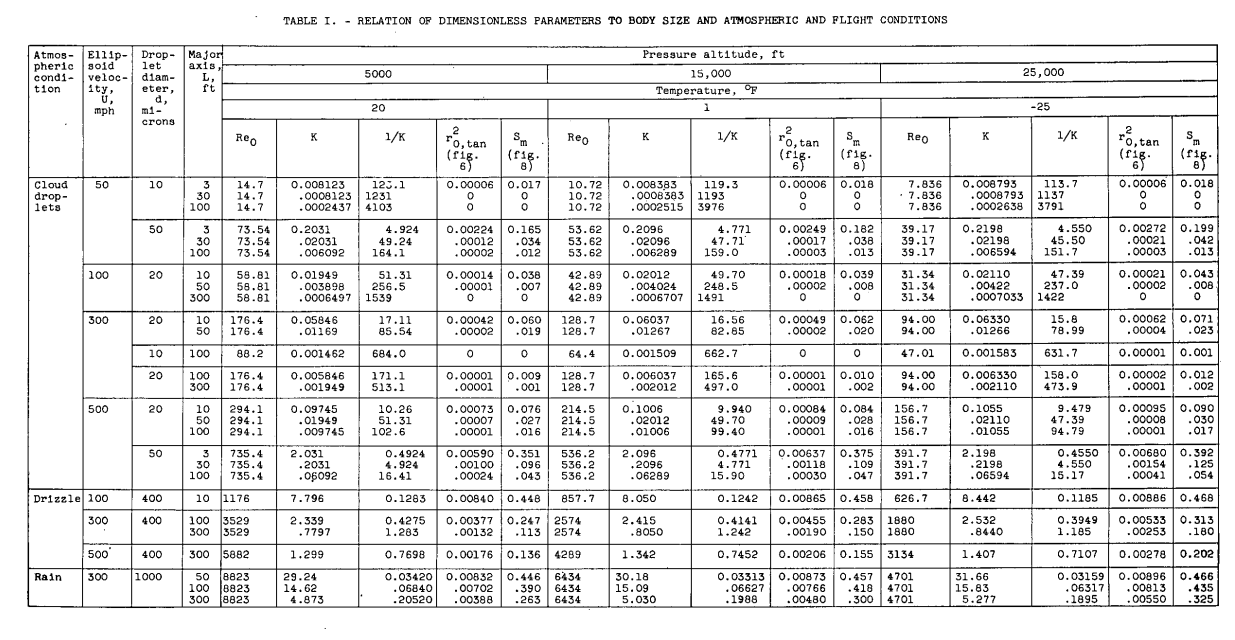
Table I. Relation of dimensionless parameters to body size and atmospheric and flight conditions.

Drop size distributions could be considered.

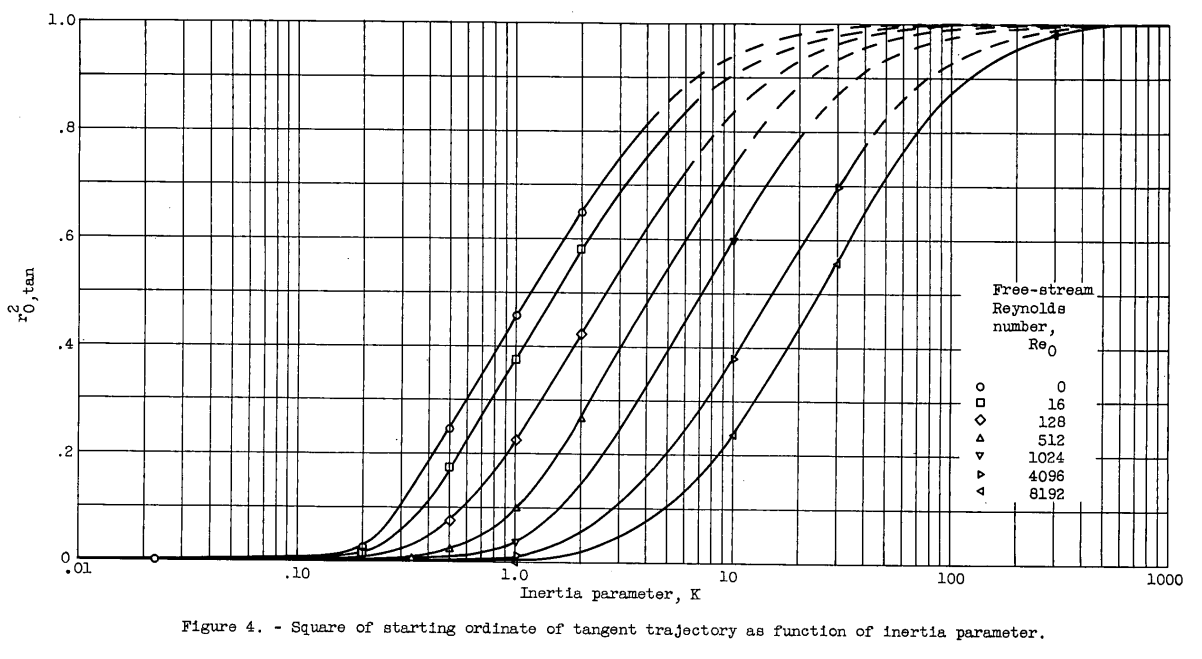
For example, consider the cloud droplet-size distribution shown in figure 11. Suppose that the volume- median droplet size is 20 microns, the velocity is 200 miles per hour, the ellipsoid length is 10 feet, the pressure altitude is 5000 feet, and the temperature is 20 F. For these conditions, the value of Re_0,med is 117.6 and of Kmed is 0.03898. The values of Re 0 and K corresponding to other droplet sizes in the distribution are obtained by multiplying Re_O med by d/dmed and Kmed by (d/dmed)^2 and are used to obtain r0^2,tan (fig. 6) for each droplet size. The values of r0^2,tan for this example are plotted as a function of cumulative volume in percent in figure 12. Integration of this curve gives a weighted value of r0^2,tan equal to 0.000425; whereas, the value based on the volume-median droplet size is 0.00031 (fig. 6).

Figure 6. Square of starting ordinate of tangent trajectory as function of inertia parameter.

Some results may be applied for similar, but not identical, bodies.

In some cases, where the body is of different shape, it may be possible to match its nose section physically with the nose section of an ellipsoid (fineness ratio, 5) of selected length. If, in such a case, the contribution of the afterbody to the air-flow field in the vicinity of the nose of the body is small (as it often is), then the impingement data for the matching portion of the surface of the ellipsoid can be used for determining the impingement characteristics of the nose region of the body. In other cases, where the body shape differs from that of an ellipsoid but the fineness ratio is the same, the air-flow field may be similar enough that an estimate of the total catch can be obtained from the ellipsoid data. In this case, no details of the surface distribution of impinging water could be obtained.

NACA-TN-3147 2 repeated a similar study for an ellipsoid of fineness ratio 10. Results were compared with those for a fineness ratio of 5 from NACA-TN-3099. By these parameters, the results appear to be similar. However, note that K is based on ellipsoid length, not diameter, so for the same diameter at the same conditions the K values will differ by a factor of 2 for the different ellipsoids.

Figure 10. Comparison of 10 and 20-percent-thick ellipsoids

NACA-TN-3587 3 has similar results for a sphere.

Figure 4. Square of starting ordinate of tangent trajectory as function of inertia parameter.

NACA-TN-4092 4 tested several bodies.

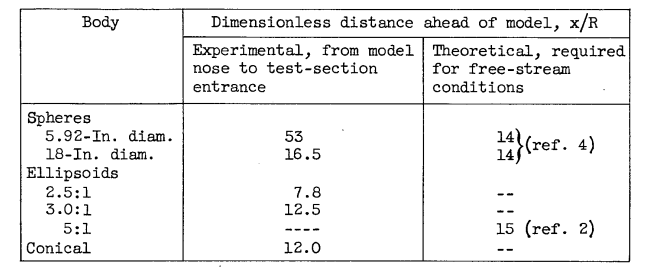
Table of test articles. Includes spheres, 5.92 and 18 inch diameter; Ellipsoids, 2.5:1, 3:1, and 5:1; and a conical section

Figure 1a. Ellipsoid body of fineness ratio 3 (20 inch diameter).
Figure 1b. Conical forebody (18.93 inch base diameter.)

Some bodies were rotated at up to 1200 rpm, but it was noted:

Although in some cases there are slight indications of an increase in impingement efficiency with rotation, in general the effect of rotation appeared to be negligible up to 1200 rpm.

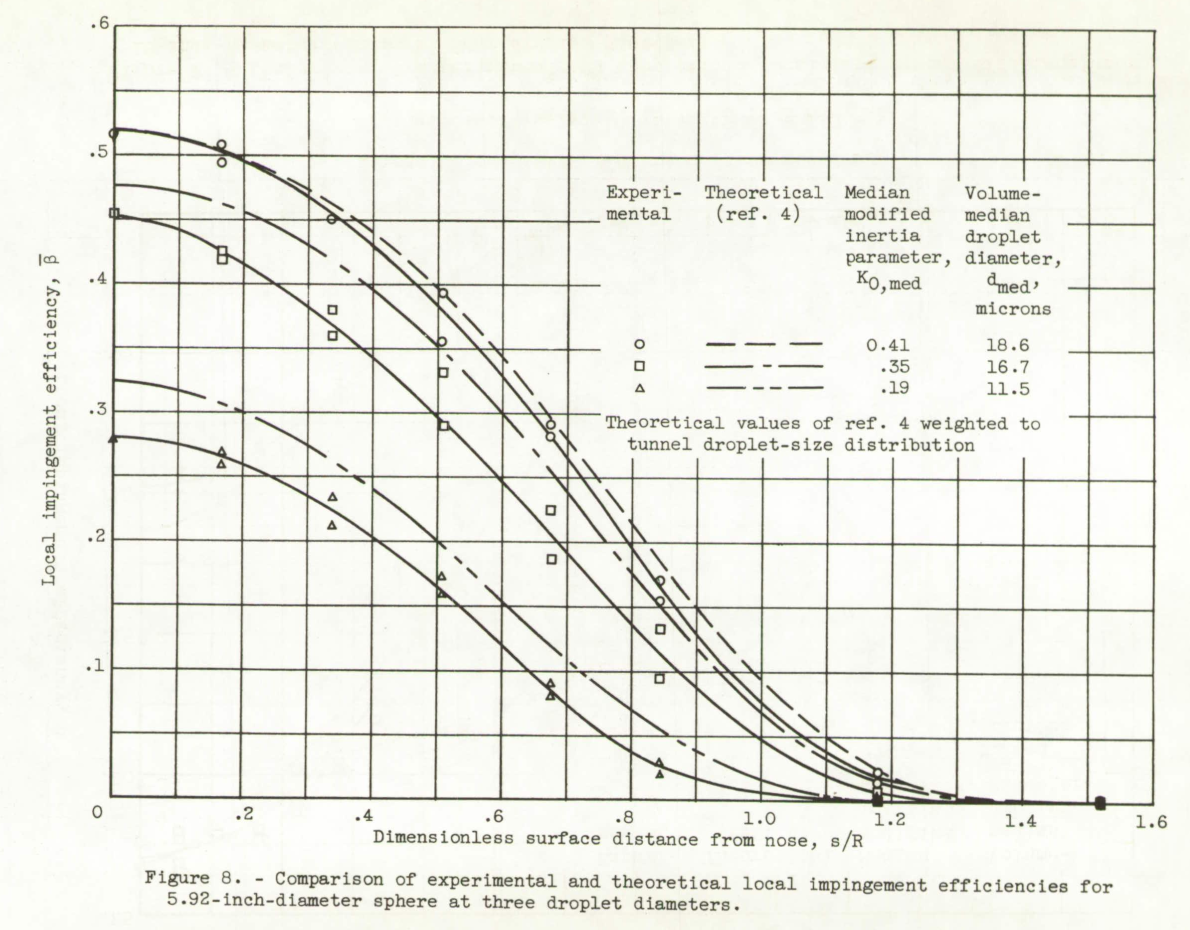
Figure 8. Comparison of experimental and theoretical local impingement efficiencies for 5.92 inch diameter sphere at three droplet diameters.

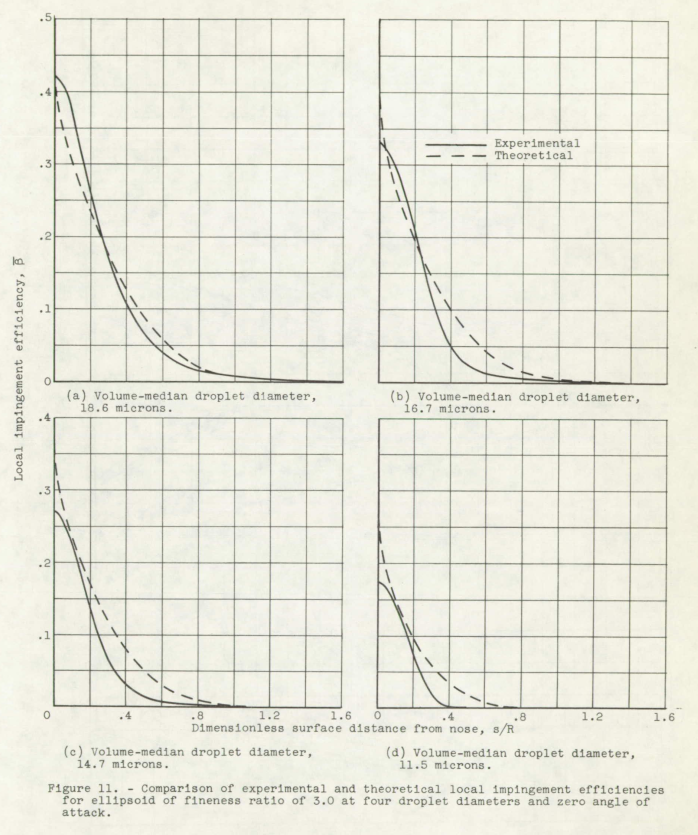
Figure 11. Comparison of experimental and theoretical local impingement efficiencies for ellipsoid of fineness ratio of 3.0 at four droplet diameters and zero angle of attack.

The effects of angle of attack were also measured (not detailed herein).

Conclusions

From NACA-TN-4092:

In general, the experimental data show that the local and total impingement rates and impingement limits of bodies of revolution are primarily functions of the modified inertia parameters, the body shape, and fineness ratio. Both the local impingement rate and impingement limits depend upon the angle of attack. Rotation of the bodies had a negligible effect on the impingement characteristics except for an averaging effect at angle of attack. For comparable diameters the bluffer bodies had the largest total impingement efficiency, but the finer and sharper bodies had the largest values of maximum local impingement efficiency and, in most cases, the largest limits of impingement. In most cases, the impingement characteristics were less than those calculated from theoretical trajectories; in general, however, fairly good agreement was obtained between the experimental and theoretical impingement characteristics.

Citations

From scholar.google.com:

NACA-TN-3099 29 citations
NACA-TN-3147 (google could not find any)
NACA-TN-3587 1 citation
NACA-TN-4092 18 citations

Related

This is part of the Water Drop Impingement on Surfaces thread.

Notes

  1. Dorsch, Robert G., Brun, Rinaldo J., and Gregg, John L.: Impingement of Water Droplets on an Ellipsoid with Fineness Ratio 5 in Axisymmetric Flow. NACA-TN-3099, 1954. ↩↩

  2. Brun, Rinaldo J., and Dorsch, Robert G.: Impingement of Water Droplets on an Ellipsoid with Fineness Ratio 10 in Axisymmetric Flow. NACA-TN-3147, 1954. ↩

  3. Dorsch, Robert G., Saper, Paul G., and Kadow, Charles F.: Impingement of Water Droplets on a Sphere. NACA-TN-3587, 1955. ↩

  4. Lewis, James P., and Ruggeri, Robert S.: Experimental Droplet Impingement on Four Bodies of Revolution. NACA-TN-4092, 1957. ↩↩

social