"Rotational speeds up to 1200 rpm had no apparent effect on the heat-transfer characteristics of the spinner"

"Investigation of Heat Transfer from a Stationary and Rotating Conical Forebody"

Abstract

The convective heat transfer from the surface of a conical forebody having a hemispherical nose, an included angle of approximately 30°, and a maximum diameter of 18.9 inches was investigated in a wind tunnel for both stationary and rotating operation. The range of test conditions included free-stream velocities up to 400 feet per second, rotational speeds up to 1200 rpm, and. angles of attack of 0° and 6°. Both a uniform surface temperature and a uniform heater input power density were used.

The Nusselt-Reynold's number relations provided good correlation of the heat-transfer data for the complete operating range at 0° angle of attack with and without spinner rotation, and for 6° angle of attack with rotation. Rotational speeds up to 1200 rpm had no apparent effect on the heat-transfer characteristics of the spinner. The results obtained at 6° angle of attack with rotation were essentially the same as those obtained at 0° angle of attack without rotation. The experimental heat-transfer characteristics in the turbulent flow region were consistently in closer agreement with the results predicted for a two-dimensional body than with those predicted. for a cone. For stationary operation at 6° angle of attack, the measured heat-transfer coefficients in the turbulent flow region were from 6 to 13 percent greater on the lower surface (wind-ward side) than on the upper surface (sheltered side) for corresponding surface locations. The spinner-nose geometry appeared to cause early boundary-layer transition. Transition was initiated at a fairly constant Reynolds number (based on surface distance from nose) of 8.0X10^4. Transition was completed at Reynolds numbers less than 5.0x10^5 for all conditions investigated.

Discussion

INTRODUCTION

Fundamental information on the heat-transfer and boundary-layer characteristics of stationary and rotating simple bodies of revolution is needed to design icing protection systems for all-weather aircraft.

Examples of simple three-dimensional bodies used as aircraft components are radomes, forward sections of external stores, propeller spinners for turboprop engines, and jet-engine accessory housings. Several theoretical and experimental heat-transfer studies have been maie for such bodies, but the data are generally limited to specific problems, such as supersonic flight, small or zero angles of attack, or zero rotational speeds.

As part of a general experimental program conducted at the NACA Lewis laboratory on icing protection for bodies of revolution, the present investigation is a study of the heat transfer from the surface of a conical forebody in clear air for low subsonic flight speeds, with and without rotation, and for angle-of-attack operation. This work is an extension of heat-transfer studies reported in references 1 and 2 for two ellipsoidal bodies of revolution having fineness ratios of 3.0 and 2.5.

APPARATUS AND PROCEDURE

The study of heat transfer from the surface of a conical forebody was conducted in the 6- by 9-foot test section of the Lewis icing research tunnel. Figure 1 is a photograph of the model installed in the tunnel. The faired afterbody and its related equipment for obtaining temperature and pressure measurements with rotation is the same as that used in previous heat-transfer studies of ellipsoids (refs. 1 and 2). The 18.9-inch maximum diameter of the conical model was faired to the 20-inch minimum diameter of the afterbody by a transition piece that rotated with the model.

The conical model proper, hereinafter referred to as a "cone" or "spinner", had an axial length of 35 inches and was constructed of 0.061- inch aluminum spun to the desired shape. The nose, or apex, of the cone was rounded to a 1/2-inch radius and the spinner surface was slightly convex (bulged), deviating from a true conical surface by approximately 0.6 inch at the midpoint. Approximately 1000 square inches of heated surface area were provided by means of internal electric heaters of the blanket type. Although the spinner model was not a true cone, it was considered adequately representative, especially for a practical installation employing blanket-type heaters. It should be stated that the model, supplied by the U. S. Air Force, was not designed and built for the specific purpose of obtaining detailed basic heat-transfer information, but rather was a production article in many respects.

A schematic drawing of the spinner model, heater layout, details of heater construction, and thermocouple cross-sectional locations are shown In figure 2. The thermocouples located within the heater proper were used to determine heat losses to the cone interior.

Method of Analysis

The heat flow paths assumed for the calculations are shown in figure 3. The external convective heat-transfer coefficient h was evaluated on the basis of an effective local heat dissipation from the external surface, neglecting in most cases longitudinal and circumferential heat conduction through the model skin Qal, but in all cases accounting for heat loss to the cone interior Qi. The heat loss to the interior of the model was determined from the relation

Qi = 28.8 (th - ti), Btu/(hr)(sq ft)  (2)  

RESULTS AND DISCUSSION

Velocity Distribution

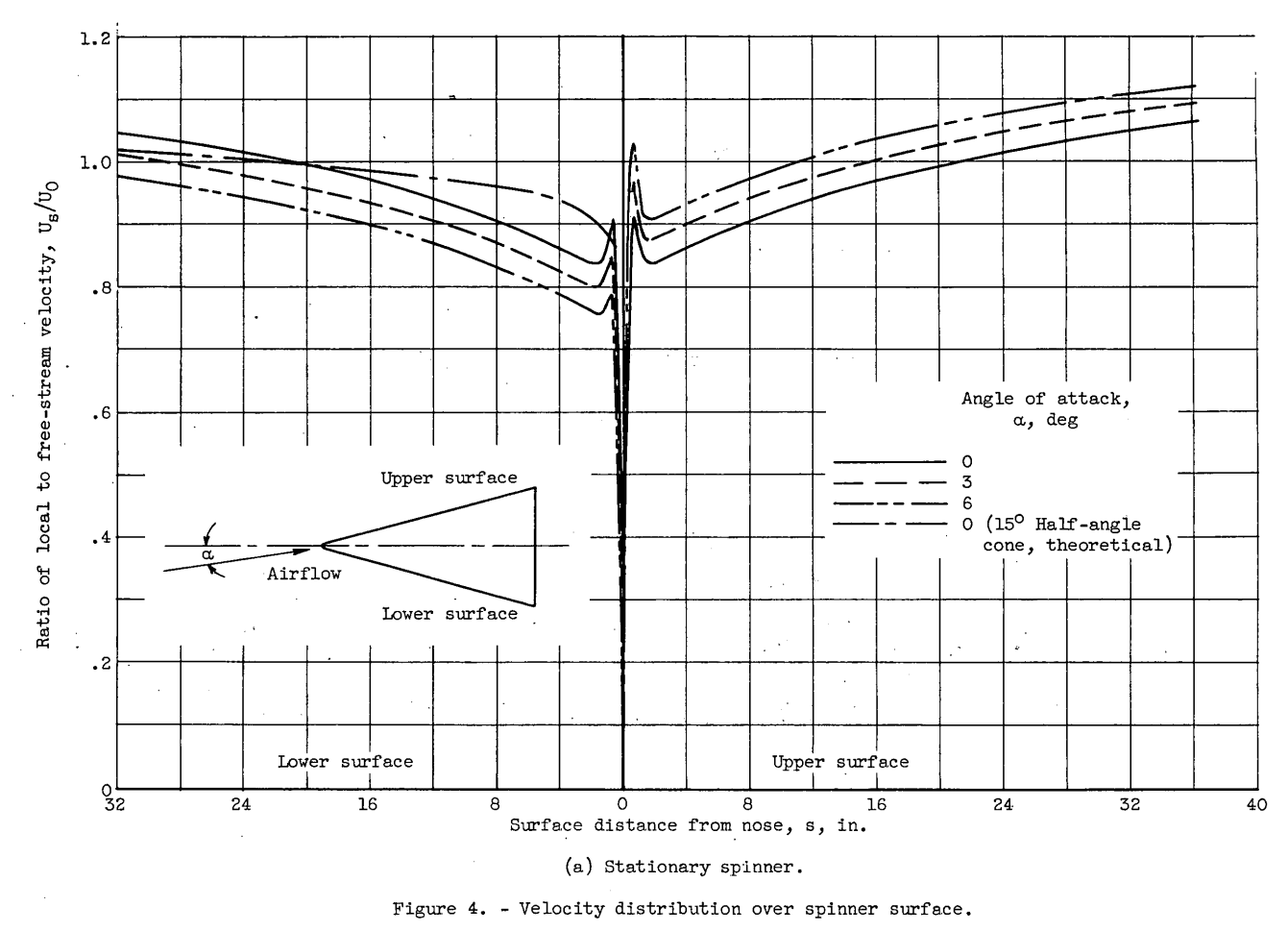
The velocity distribution over the surface of the cone for zero rotation is presented in figure 4(a) in terms of the ratio of local to free-stream velocity Us/U0 for three angles of attack. For the conditions investigated, the sharp peak in velocity occurred at a constant value of 0.7 inch from the spinner nose, which corresponds to the point at which the cone body becomes tangent to the hemispherical nosecap. The shift in air stagnation point was found to be very small (less than 1/8 inch at 6°) and was neglected in computations involving local surface distance. The theoretically predicted velocity distribution (ref. 9) for a true 15° half-angle cone at 0° angle of attack is presented for comparison with experimental results. Measurements in a meridional plane midway between the upper and lower surfaces for 6° angle of attack (stationary) showed local velocities in this plane to be only 1.5 to 3.0 percent lower than those obtained for the upper, or sheltered, surface.

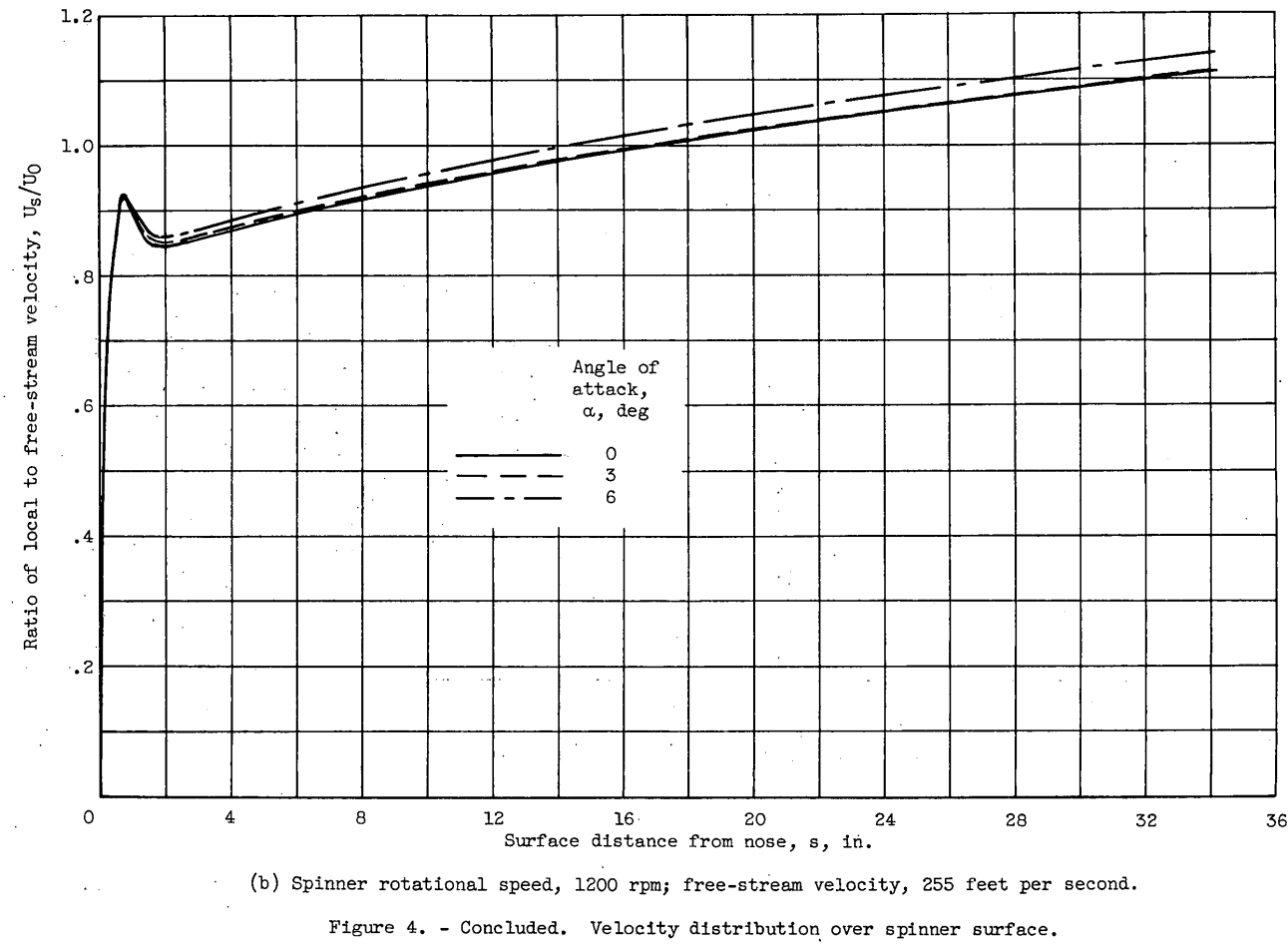
Velocity distributions with spinner rotation are presented in figure 4(b) for 0°, 3°, and 6° angles of attack. These curves are for the maximum rotational speed and minimum free-stream velocity investigated (1200 rpm and 255 ft/see, respectively). The results show that, with spinner rotation, velocity distribution is rather insensitive to small changes in angle of attack. In addition, comparison of figures 4(b) and 4(a) shows that rotation at 0° angle of attack caused a maximum increase in local velocity of only about 5 percent at the rear of the spinner.

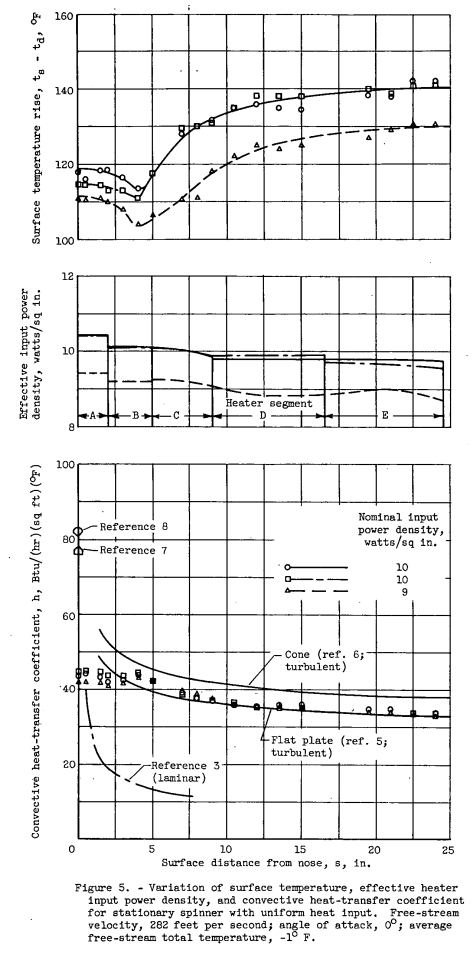
Typical results. - Typical data obtained at 00 angle of attack with uniform heat input (nonuniform surface temperature) are presented in figure 5 in terms of the surface temperature rise ts - td and the convective heat-transfer coefficient h for two values of input power density. The data (from nonconsecutive runs) are for a stationary spinner and exemplify the general characteristics and repeatability of results for the condition of uniform heat input.

Also shown in figure 5 is the variation of effective heater power density (input power minus loss to the cone interior) with surface distance from the nose. The decrease in effective heater power density with increasing surface distance is indicative of the heat loss to the cone interior since the input density was essentially uniform. The internal heat loss ranged from a minimum of approximately 3 percent to a maximum of about 10 percent of the total heat input. The rate of heat loss to the cone interior increased steadily with increasing surface distance from the nose except for heaters A and B, where measured temperatures indicated negligible internal heat loss in all cases.

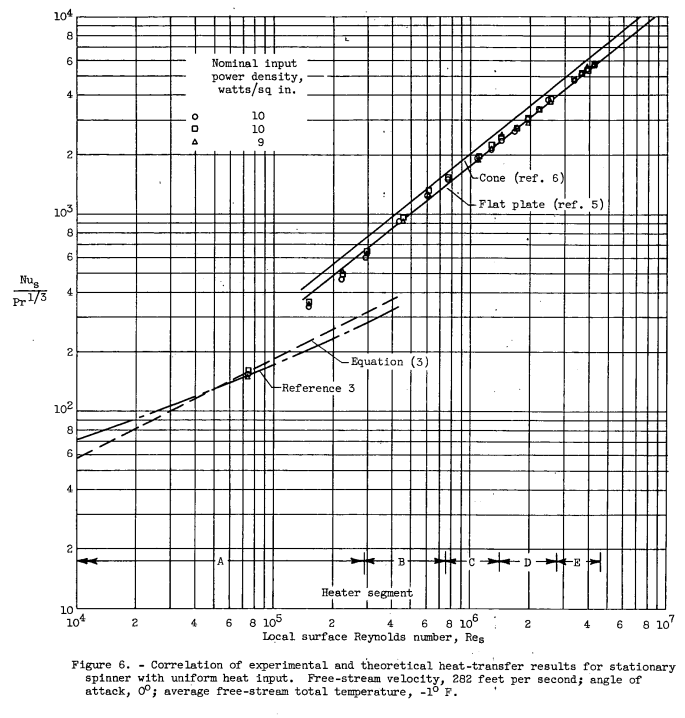
In the present model, however, the hemispherical nosecap extends to only about 75° from stagnation, at which point it attaches to the conical body. Hence, for the data presented in figure 6 (Re d l.8xl05 ), the maximum extent of laminar flow probably cannot exceed Re 5 i05 (local surface Reynolds number corresponding to 75° on the nosecap). Although initiation of transition appears to result from the nature of the flow about the nosecap, the abrupt change in pressure gradient probably destabilizes the boundary layer further and thus completes transition in a relatively short distance. For higher free-stream velocities, the laminar region may be expected to be even less than that noted for the data in figure 6.
Because the region of laminar flow was extremely small, the heat-transfer results for this region were limited to data obtained from a single measuring station (data for Re 8 = 7.3x104 , fig. 6). These data cannot adequately describe the heat transfer in the laminar region and, hence, the order of agreement between experimental and. predicted results cannot be definitely stated. Although the results appear to agree quite well with predicted values, this fact may be fortuitous in view of the nature of the heat-transfer results previously described for the nose section, that is, essentially constant values of heat-transfer coefficient and surface temperatures. Because the measured surface temperatures were always practically constant for heater A area (even for the case of uniform heat input), the theoretical results of reference 3 were determined on the basis of uniform surface temperature only.

Conclusions

SUMMARY OF RESULTS

An experimental wind-tunnel investigation of heat transfer from the surface of a conical forebody (18.9-in. maximum diameter) operating under stationary, rotating, and angle-of-attack conditions yielded the following results:
1. Good correlation of th heat-transfer results was obtained by use of the Nusselt-Reynolds number relation for the complete operating range investigated for 0° angle of attack with and. without spinner rotation, and. for angles of attack up to 6° with rotation.
2. Rotational speeds up to 1200 rpm had no apparent effect on the heat-transfer characteristics of the spinner. The heat-transfer data at angle of attack with rotation were essentially the same as those obtained at 0° angle of attack without rotation.
3. Heat-transfer results in the region of turbulent boundary-layer flow were consistently in closer agreement with the values predicted for two-dimensional bodies than with those predicted for a cone.
4. For stationary operation at 6° angle of attack, the measured values of heat-transfer coefficient in the turbulent region were from 6.0 to 13.0 percent less on the sheltered side (upper surface) than those on the windward side (lower surface) for corresponding surface locations.
5. Early boundary-layer transition occurred for all conditions investigated. Transition was initiated at a fairly constant value of local Reynolds number (based on surface distance from nose) of 8.0X10^4. In all cases, the transition from laminar to turbulent flow was completed at Reynolds numbers less than 5.0X10^5.

Citations

This publication is cited by two publications, per scholar.google.com.

Related

This is part of the Engine Inlet Icing Thread.

Notes