"Many aircraft components are essentially simple bodies of revolution; examples of these are radomes, body noses, engine accessory housings, and the large spinners of turboprop engines"

"Investigation of Heat Transfer from a Stationary and Rotating Ellipsoidal Forebody of Fineness Ratio 3" ¹

Abstract

The convective heat transfer from the surface of an ellipsoidal fore-body of fineness ratio 3 and 20-inch maximum diameter was investigated in clear air for both stationary and rotating operation over a range of conditions including air speeds up to 240 knots, rotational speeds up to 1200 rpm, and angles of attack of 0°, 3°, and 6°. The results are presented in the form of heat-transfer coefficients and the correlation of Nusselt and Reynolds numbers. Both a uniform surface temperature and a uniform input heater density distribution were used.

The experimental results agree well with theoretical predictions for uniform surface temperature distribution. Complete agreement was not obtained with uniform input heat density in the laminar-flow region because of conduction effects. No significant effects of rotation were obtained over the range of airstream and rotational speeds investigated. Operation at angle of attack had only minor effects on the local heat transfer. Transition from laminar to turbulent heat transfer occurred over a wide range of Reynolds numbers. The location of transition depended primarily on surface roughness and pressure and temperature gradients. Limited transient heating data indicate that the variation of surface temperature with time followed closely an exponential relation.

Discussion

INTRODUCTION
In the general field of design of modern all-weather aircraft, the problem of protecting bodies of revolution against icing has become of increasing importance. Many aircraft components are essentially simple bodies of revolution; examples of these are radomes, body noses, engine accessory housings, and the large spinners of turboprop engines. The design of thermal icing protection systems for these components requires knowledge of the heat-transfer relations for both stationary and rotating bodies of revolution. Such information is of interest also in the general field of heat transfer. Several theoretical studies of the problem have been made (refs. 1 and 2). However, very little experimental heat-transfer data for such bodies are available and the data are generally of limited scope.

Experimental investigations have been made at the NACA Lewis laboratory of the heat transfer from bodies of revolution in order to obtain more extensive data than are presently available, including the effects of angle of attack and rotation. The investigation was made as part of a general study of icing and icing protection of bodies of revolution. This report presents the results of an investigation of the heat transfer in clear air from the surface of an ellipsoidal forebody of fineness ratio 3 and a 20-inch maximum diameter. Similar results for a larger-diameter ellipsoidal forebody of fineness ratio 2.5 are reported in reference 3.

In the present study the steady-stage convective heat transfer was determined with and without rotation of the ellipsoidal forebody over a range of airspeeds up to 240 knots, rotational speeds up to 1200 rpm, and angles of attack of 0°, 3°, and limited transient heating data were also obtained. Heat was provided by an internal electric heater designed and instrumented to yield as much basic heat-transfer data as possible while at the same time preserving the performance and constructional details of a representative practical heater installation.

APPARATUS

The model, consisting of half of an ellipsoidal body of revolution with a half major axis of 30 inches and a half minor axis of 10 inches, was mounted on a faired afterbody in the 6- by 9-foot test section of the Lewis icing research tunnel (fig. 1). The test model proper, consisting of the ellipsoidal forebody, is hereinafter referred to as the spinner model to distinguish it from the entire assembly. The afterbody, power-supply system, thermocouple pickup, and temperature recording system were essentially the same as used in the tests of reference 3. The spinner model was fabricated of 0.062-inch aluminum spun in one piece to the desired shape. An ogive transition section 15 inches long faired the contour between the rear of the 2O-inch-dianieter spinner and the 30-inch diameter afterbody. The rear of the spinner model was located at the same position relative to the afterbody as was the rear of the 30-inch-diameter spinner of reference 3. Heat was supplied to the spinner by electric heaters located on the inside surface of the spinner shell.

The spinner contour, heater layout, and details of the heater construction and thermocouple installation are shown in figure 2. The heater was divided into eight areas, each constituting a single circuit connected to separate autotransformers permitting selective control of heat density and axial heat distribution. The heat input to each heater area was measured by a voltmeter and an ammeter. The spinner surface area for each heater is listed in table I. The longitudinal heaters (G and H) were located on two diametrically opposite sides of the spinner; these heaters were designed to provide parting areas for subsequent cyclic de-icing tests.

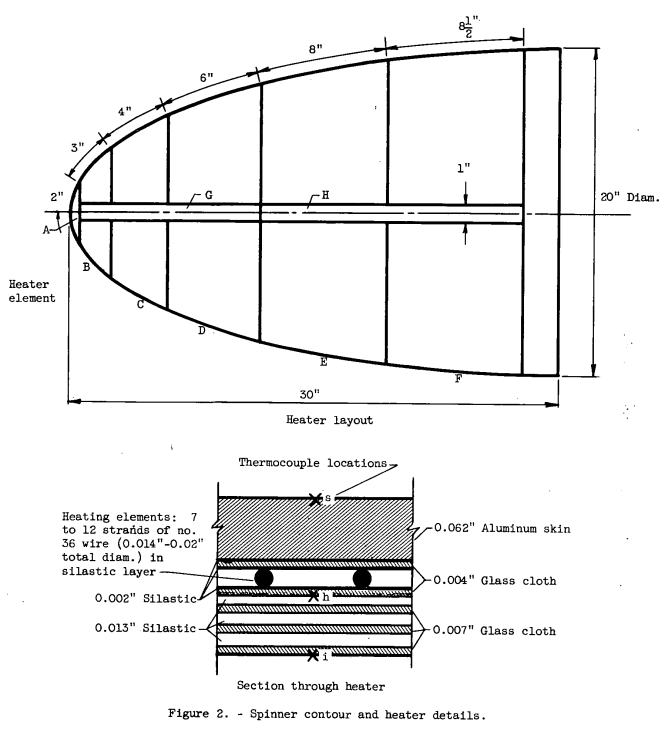
The heating elements consisted of strands of 36-gage Nichrome heating wires encased between plies of glass cloth and silastic (silicone plastic). The highier temperature limit of the silicone compared with the neoprene insulation used in the heaters of reference 3 permitted operation at higher skin temperatures and heat densities. Copper-constantan thermo-couples were installed at various locations to obtain both the skin temperature distribution and the inward heat dissipation. A sketch of the system used to transmit the temperatures from the thermocouples to the recorder is shown in figure 3(a). Details of the operation of this system are given in reference 4.

Method of Analysis

Experimental data. - The experimental results are presented in terms of the heated-surface temperature rise above the unheated-surface equilibrium temperature ts - td, the external convective heat-transfer coefficient H, and the local Nusselt number Nu_s.

The convective heat-transfer coefficient was computed from the following relations:

H = Qs / (A ( t - td))
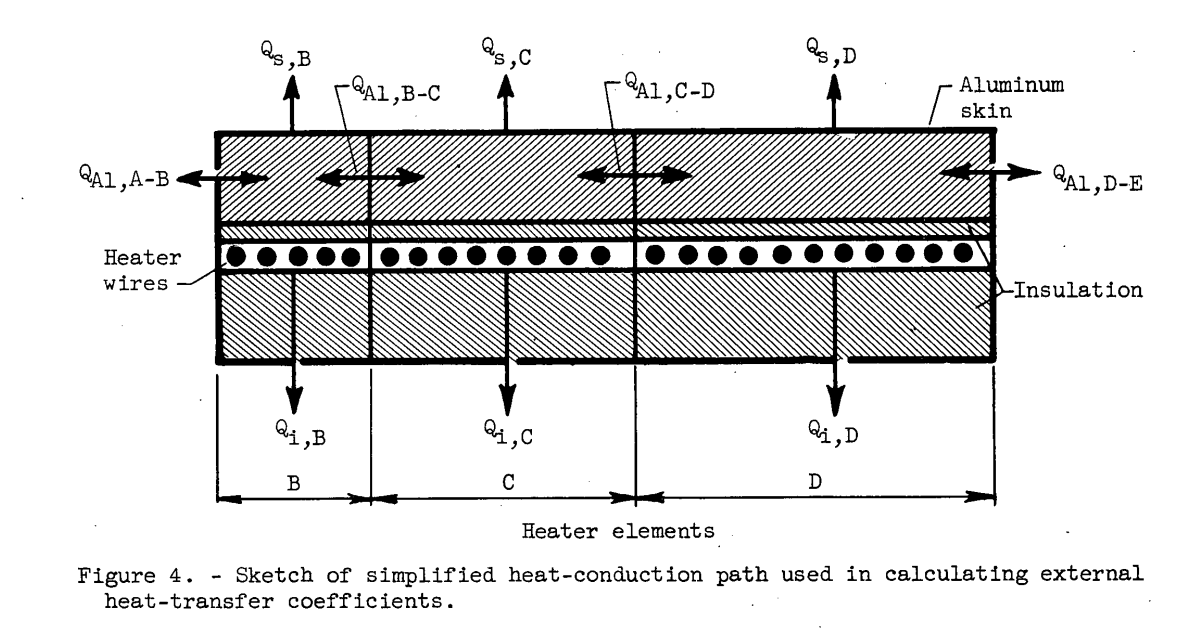
Qs = Q - Qi ± QAl

A sketch of the assumed heat flow from the heater is shown in figure 4.

RESULTS AND DISCUSSION

Velocity Distribution

The local velocity over the spinner surface is required in the cor- relation of the heat-transfer data. In addition, a comparison of the measured velocity distribution with theoretical values indicates the magnitude of any tunnel effects and, hence, the validity of the tunnel simulation. The ratio of the local velocity to the free-stream velocity is presented in figure 5. These data are uncorrected for tunnel effects, because this measured value is that which is required for the correlation of the heat-transfer results. A theoretical curve obtained by the method of reference 6 for nonviscous incompressible flow is also presented in figure 5(a) for an angle of attack of 0°.

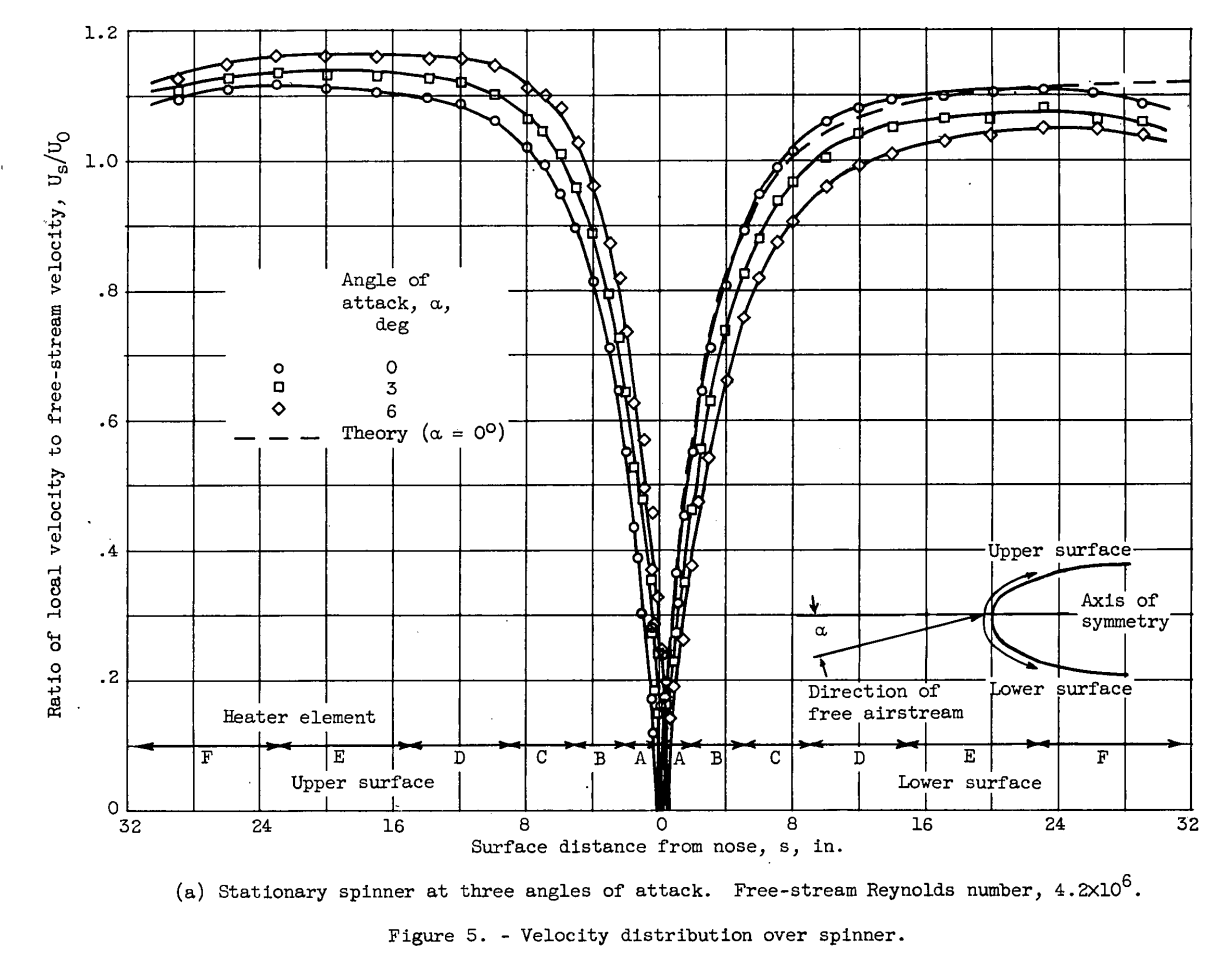
The experimental data over most of the spinner surface agree well with the theoretical curve.

The local velocity distribution for the rotating spinner is compared with the results for the stationary spinner in figure 5(b) at an angle of attack of 0°. No significant effect of rotation on the local velocity was obtained even at the maximum rotational speed (1200 rpm). This result might be expected, since the local velocities for the stationary spinner are only 5 percent less, at the most, than the local velocities computed as the resultants of the longitudinal and rotating components.

Steady-State Heat-Transfer Results

The steady-state heat-transfer results are discussed first in terms of a general correlation of the results for the separate cases of uniform surface temperature and uniform input power density, and secondly in relation to the specific effect of the several operating variables.

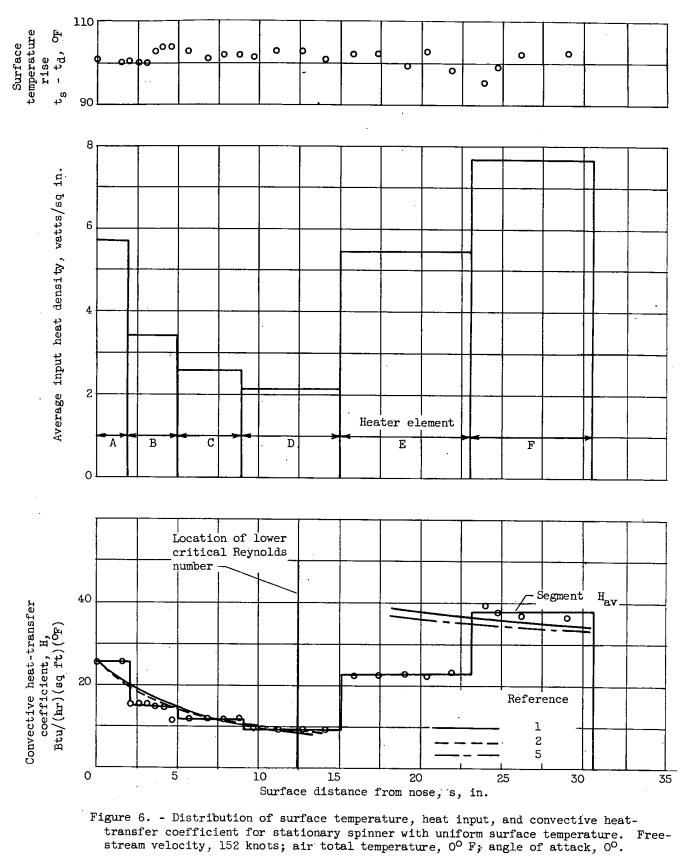
Uniform surface temperature. - Typical results obtained with a uniform surface temperature are shown in figure 6. The surface temperature rise, ts - td, heater input power density, and convective heat-transfer coefficient are given for the stationary spinner at 00 angle of attack. (The measured unheated equilibrium surface temperature was essentially constant over the body surface for all tests.) The data of figure 6 were obtained with the spinner surface in its smoothest condition. The segment average coefficient is shown by the stepped straight lines, while the data points are the local effective coefficients. The experimental heat-transfer coefficients agree well with the theoretical stagnation, laminar, and turbulent values. A fairly extensive region of laminar flow was obtained, with transition starting approximately 13 inches from the nose and a fully turbulent condition reached at approximately 24 inches from the nose. Included in figure 6 is the value of the lower critical Reynolds number of boundary-layer stability calculated from the analysis of Schlichting. For values less than the critical the boundary layer is assumed stable, and transition does not occur in the absence of surface roughness or other disturbing effects. Transition and boundary-layer stability are discussed later. Both the surface temperatures and heat-transfer coefficients reflect the unfaired stepped heat distribution.

The heat-transfer results of figure 6 are shown in the Nusselt, Prandtl, and Reynolds number form in figure 7. In terms of the local Reynolds number Re_s, transition began at approximately 2.3 X 10^6 and was completed at approximately 4.2 X 10^6 . Fairing of a smooth curve through the heat-rate distribution would reduce the spread of the data to approximately 10 percent, and the experimental data would vary less than 10 percent from the theoretical values.

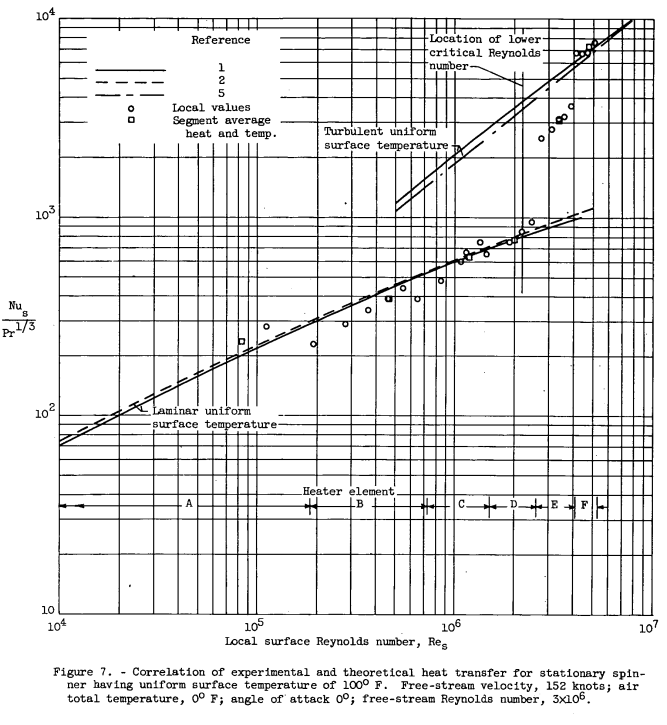
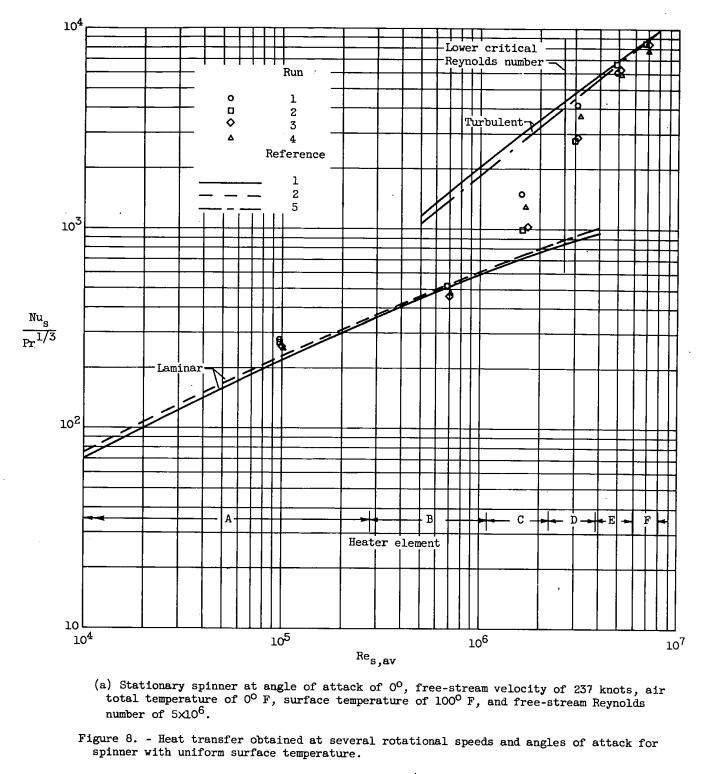
The heat transfer at several angles of attack and rotational speeds for the spinner with a uniform surface temperature is compared in figure 8. The results of several repeat runs made with the stationary spinner at 0° angle of attack (fig. 8(a)) indicate good reproducibility of data and agree well with the theoretical values. These data are similar to those obtained at a lower stream Reynolds number (fig. 7), except that the local Reynolds number of transition is lower in figure 8(a). This forward movement of transition is attributed to the increased surface roughness in the region of rapidly decreasing velocity gradient (s > 5 in.) rather than the increased stream Reynolds number or stream turbulence. During the progress of the tests the entire surface gradually became roughened by foreign particles in the tunnel airstream, although the spinner surface was hand-sanded lightly at intervals throughout the course of the investigation in an effort to keep the degree of surface roughness fairly constant.

Conclusions

From a study of the convective heat transfer from an ellipsoidal forebody of fineness ratio 3 in clear air, the following results were obtained:
1. The experimental heat-transfer coefficients for the case of a uniform surface temperature agreed well with the theoretical predictions of Drake, Squire, and Martinelli for the stagnation, laminar, and turbulent heat-transfer regions. Complete agreement in the laminar-flow region for the case of uniform input heat density was not obtained because of conduction effects. 2. Good correlation of the experimental results for all operating conditions was obtained by the use of the Nusselt-Prandtl-Reynolds number relation. No significant effects of rotation on the heat-transfer coefficients or transition were obtained for the range of rotational and airstream speeds investigated. Operation of the spinner at angles of attack up to 6° had only minor effects on the heat transfer, primarily causing a movement of transition in accordance with changes in the local velocity distributions. The time-averaged heat-transfer coefficients obtained at angle of attack with rotation of the spinner were essentially the same as obtained at 0° angle for the stationary spinner. 3. The heat-transfer results for the stationary spinner agreed well with those obtained with a 30-inch-diameter fineness ratio 2.5 spinner. 4. Transition from laminar to turbulent heat transfer occurred over a wide Reynolds number range, including both the movement of beginning of transition and also the extent of the transition region. The beginning of transition varied from a local surface Reynolds number of approximately O.8 X106 to 2.3 X 106 (corresponding to a boundary-layer Reynolds number between 200 and 600), depending upon surface roughness and pressure and temperature gradients. Beginning of transition did not occur forward of 3 to 4 inches from the nose. The end of transition varied over a local surface Reynolds number range of approximately 3 X 10^6 to 5 X 10^6 . The effects of rotation and angle of attack on transition Reynolds number were negligible. 5. Transient heating data were obtained which indicated that the variation of surface temperature with time was essentially an exponential relation. The relatively large thermal capacity of the heater-spinner configuration caused a large temperature-time lag, as indicated by external surface time constants of approximately 50 to 80 seconds for both heating and cooling.

Citations

NACA-TN-3837 is cited 11 times, per scholar.google.com.

Related

There is also

• von Glahn, Uwe H.: Preliminary Results of Heat Transfer from a Stationary and Rotating Ellipsoidal Spinner. NACA-EM-E53F02, 1953.

However, this largely a preliminary version of NACA-TN-3837, and so it will not be separately reviewed.

This is part of the Engine Inlet Icing Thread.

Notes