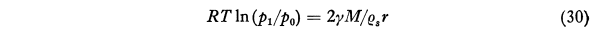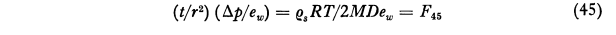"It is possible to develop this theory to cover also growth of water droplets during the adiabatic expansion of a rising mass of saturated air."

Irving Langmuir, "Super-Cooled Water Droplets in Rising Currents of Cold Saturated Air"

Summary

Evaporation and condensation rates on water drops are calculated.

Key Points

1. A theory of water drop growth by condensation in the atmosphere is developed.
2. The drop size measurement by oiled-slide and multicylinder instruments is improved.
3. The evaporation rates of stationary water drops is analyzed.

Abstract

As this is an extensive work (130 pages), and as Langmuir did not provide an abstract or introductory summary, we will begin with the Langmuir's conclusions as a summary.

Summary of Main Conclusions of Part I to April 1, 1944

Before analyzing the new data it is desirable to summarize the main conclusions reached from the foregoing parts of this report:

1. The Glauert theory of the deposition of rime on a cylinder, giving the weight, width, and thickness of rime as a function of the wind velocity, the particle size and the cylinder radius, gives reasonably consistent values for the droplet radius when the theory is applied to the March, 1943 Mt. Washington data. Unfortunately, only one rotating cylindrical rime collector was used, the other two being stationary. As the rime deposited on the stationary collectors these soon became non-circular in cross section. In many cases it was necessary to reject data for this reason. The droplet radius calculated by the application of the Glauert riming theory will be denoted by r_R.
2. A theory of the growth of droplets in rising saturated air was developed, according to which the smaller drops in the fog evaporate even while the liquid water content of the fog continues to increase. As the drops grow in size their number steadily decreases. A quantitative development leads to the conclusion that the radius of the droplets depends only on the temperature and age of the fog, i.e. the time during which the fog particles have been in existence. The droplet radius does not depend directly on the liquid water content but rather on the ratio of this to the vertical component of the velo- city of the air entering the base of the cloud. The droplet radius calculated from this time of rise or aging theory we will call r_t.
3. A comparison of r_R and r_t , given by the riming and the time of rise theories from the same data show excellent agreement. The logarithmic correlation coefficient (LCC) which measures the correlation between log r_R and the log r_t was found to be +.92 (see pages 235 to 236 of this Report). The average deviation between the values of r_t and r_R is only slightly over 20 per cent although the radius varied over a range over 1 to 10. Actually it was found that r increased a little more rapidly than in proportion to r_R. This high correlation between r_R and r_t gives strong support to the Glauert theory of rime deposition and to the proposed theory of droplet growth.
4. A theory was developed by which the droplet size is related to the product of the liquid water content of the fog and the visibility in feet. A semi-empirical equation was developed (Eq. 96) to express this relationship.
5. Microscopic observations and microphotographs to determine droplet radius by the Houghton-Radford method have been made by the Mt. Washington Observatory. It was believed that the microphotographs gave direct measurement of droplet radius. However, the radii determined in this way averaged 3.1 times as great as the value r_R given by the riming theory. In the case of the higher wind velocities and the larger droplet sizes the ratio was sometimes as high as 9.5. Others w ho have been familiar with the Mt. Washington droplet size determinations have concluded that the Glauert theory for some unknown reason gave particle sizes that were too small. Our conclusion in this Report is that the microscopic observations are faulty. The droplets appear too large because of coalescence of droplets on the vaseline covered slide. We wished particularly to test out this conclusion by further observations on Mt. Washington. Empirically we found that the quantity (55 M/v)^0.59, Eq. (99) shows a correlation (LCC) of 0.956 with r_R. In this relation M is the radius determined by direct microscopic observation and v is the wind velocity in miles per hour. The nonlinear relation between M and r_R and its dependence on wind velocity are both satisfactorily explainable by the coalescence of drops which strike the grease covered slide particularly at high velocities.
6. By using soot-covered glass surfaces or by observing the scattering of light from vaseline-coated surfaces, splash patterns were obtained when the droplets strike a surface. These experiments not only gave a quantitative relation between the splash patterns, wind velocity, and the droplet radius but they give a quantitative explanation of the reasons for the nonlinear relationship between M and r_R and the dependence on wind velocity.

Part II. New Mt. Washington Data

Part II includes two aspects that first appeared in this report, that are key to the widely cited ""Mathematical Investigation of Water Droplet Trajectories"" ².

1. "Langmuir" drop size distributions (see A Langmuir B drop size distribution is (almost) a normal distribution).
2. The Langmuir and Blodgett implementation of the equations of motion of water drop impingement on cylinders (see "Mathematical Investigation of Water Droplet Trajectories").

To summarize, Langmuir wanted to compare measured drop sizes to his water drop growth theory, found that current drop measurement methods (oiled slide, mutlicylinders) to be of limited accuracy, and so went on to develop better implementations of both methods.

Discussion

In this review, we will concentrate only on the evaporation and condensation of water vapor from and to the surface of a water drop.

The oiled-slide method of measuring water drops is described:

Estimates of radius of water droplets in a cloud were made by a method developed by H. G. Houghton and W. H. Radford. A small glass plate 5 x 5 millimeters square was exposed for a period varying from 1/2 to 2 seconds by a trigger operated shutter to the full force of the wind on the tower of the Observatory at Mt. Washington. The surface of the slide had been made hydrophobic by covering with a thin film of vaseline which was then heated to 300°C in an oven. The prepared slide, after exposure to the rime was examined microscopically. In nearly all cases the moisture was present on the slide in the form of droplets that ranged from about 5 to 75 microns radius, the average radius being roughly 40 microns. The observation of the slides was made in a little room at the tower which was at the outdoor temperature. Usually by the time the observation was made the droplets of water deposited on the slide had turned to ice.

Evaporation rates of water drops on the slide was a concern, as drop sizes could change, and small drops in particular could disappear, during the time it took to photograph the sample.

The effect of surface tension on the internal pressure of a water drop was calculated:

For a water droplet of 5μ radius at -5°C the value p1/po is 1.000247. Because of the increased vapor pressure there is a tendency for the small droplet to evaporate even in air saturated with vapor.

After much development, an equation for the time required to evaporate a drop was found. The calculated life of small drops outside of the conditions where they were formed is short.

where t is the life of a droplet which initially has the radius r. The symbol F45 denotes the function represented by the second member of Eq. (45) as tabulated in Col. 9 of Table VII. This equation is designed to facilitate the calculation of the life of a water droplet in air of any specified relative humidity Since the pressure increment Δp is the difference between the saturation vapor pressure ew and the partial pressure of water vapor in the surrounding atmosphere, 1-Δp/ew is the relative humidity. Consider, for example, a water droplet of 3μ radius in air of 60 per cent relative humidity at -10°C. We then have Δp/ew = 0.40, r = 3x10-4 cm and F45 = 7.98x105 and thus from Eq (45) Τ = 0.180 second. For particles of other sizes the life can be calculated readily since it varies in proportion to r^2. It is evident from this result that if widely separated droplets of this small size were deposited on a glass slide for microscopic examination they would disappear before observations could be made if they were brought into air of low relative humidity.

Thus the life of a droplet of 3 μ radius in air saturated with respect to snow at -10°C is only 0.79 second. The minimum value of 10-8F46 is 0.086 at -11°C but even at -40°C the life is only 4.4 times as great as at this minimum. With particles of 13 microns radius, which I believe were about the largest primary fog particles that occurred in the Mt. Washington observations as given, for example, in Col. 7 of Table III, the life at -10°C would be only 17 seconds and at -25°C, 23 seconds. The difficulty in using the Houghton Radford microscopic measurement on Mt. Washington for particles as small as this is thus apparent.

A water drop in an environment more similar to the conditions that it was formed in has a longer life:

Life of Moderately Small Droplets in Saturated Air. Thus, although the life of a particle of one micron radius at -15° would be only 6.2 seconds, a particle of 10 microns radius would be 6200 seconds, or 1.72 hours.

The growth rate of a drop in rising air was calculated.

Theory of Growth of Particles in Expanding Saturated Air.
At any stage in the formation of a cloud the droplets are not of uniform size but there is a distribution of particle sizes above and below a mean value. The smaller drops have a higher vapor pressure than the larger drops. Therefore the small drops evaporate and the moisture they contain deposits on the large drops. There is thus a continual decrease in the number of droplets. Those that remain become increasingly large. Let us assume that while this process is going on, the distribution of the particles among the various size groups, (each being defined in terms of the radius), expressed as a fraction of the mean radius, remains substantially unchanged. Thus, for example, the percentage of the particles that have radii less than 0.8 of the mean radius remains constant while the particles gradually increase in diameter. It is not probable that this condition is strictly fulfilled, but rough analysis indicates that the effects we are looking for are not very sensitive to moderate changes in the distribution function. We shall, therefore, assume that the distribution function remains constant. In any given time interval the fraction of the particles that disappears should then vary inversely in proportion to the life-time of the droplets of average size.

It is possible to develop this theory to cover also growth of water droplets during the adiabatic expansion of a rising mass of saturated air.

Langmuir considered the case of mass transfer by diffusion (only), and so for the evaporation calculations the relative airspeed of the water drop is considered to be zero, so a convective mass coefficient is not used.

An equation for the time required to evaporate a drop was found. The calculated life of small drops outside of the conditions where they were formed is short.

where t is the life of a droplet which initially has the radius r. The symbol F45 denotes the function represented by the second member of Eq. (45) as tabulated in Col. 9 of Table VII. This equation is designed to facilitate the calculation of the life of a water droplet in air of any specified relative humidity Since the pressure increment Δp is the difference between the saturation vapor pressure ew and the partial pressure of water vapor in the surrounding atmosphere, 1-Δp/ew is the relative humidity. Consider, for example, a water droplet of 3μ radius in air of 60 per cent relative humidity at -10°C. We then have Δp/ew = 0.40, r = 3x10-4 cm and F45 = 7.98x105 and thus from Eq (45) Τ = 0.180 second. For particles of other sizes the life can be calculated readily since it varies in proportion to r^2. It is evident from this result that if widely separated droplets of this small size were deposited on a glass slide for microscopic examination they would disappear before observations could be made if they were brought into air of low relative humidity.

Thus the life of a droplet of 3 μ radius in air saturated with respect to snow at -10°C is only 0.79 second. The minimum value of 10-8F46 is 0.086 at -11°C but even at -40°C the life is only 4.4 times as great as at this minimum. With particles of 13 microns radius, which I believe were about the largest primary fog particles that occurred in the Mt. Washington observations as given, for example, in Col. 7 of Table III, the life at -10°C would be only 17 seconds and at -25°C, 23 seconds. The difficulty in using the Houghton Radford microscopic measurement on Mt. Washington for particles as small as this is thus apparent.

For conditions similar to those the drop developed in, the calculated life is longer:

Life of Moderately Small Droplets in Saturated Air. Thus, although the life of a particle of one micron radius at -15° would be only 6.2 seconds, a particle of 10 microns radius would be 6200 seconds, or 1.72 hours.

Predicted drop sizes r_t are shown in Table IX.

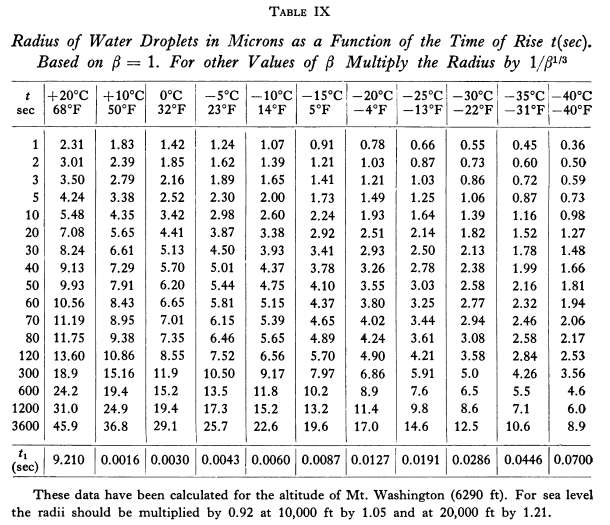
Adiabatic lift theory was then used to determine the time value t.

Conclusions

Care must be taken when using the oiled-slide method to ensure that drops do not evaporate or coalesce.

Water drops of "typical" cloud sizes (10 micrometer diameter) at low relative airspeeds in saturated humidity have low evaporation rates, with a calculated life of almost 2 hours.

Citations

Langmuir cites 8 references:

• Glauert, Muriel: A Method of Constructing the Paths of Raindrops of Different Diameters Moving in the Neighbourhood of (1) a Circular Cylinder, (2) an Aerofoil, Placed in a Uniform Stream of Air; and a Determination of the Rate of Deposit of the Drops on the Surface and the Percentage of Drops Caught. R. & M. No. 2025, British A.R.C., 1940.
• "On the measurement of drop size in liquid water content in fogs and clouds", Papers in Physical Oceanographic Institute and Meteorology, published by Mass. Inst. of Tech. and Woods Hole Oceanographic Institute, Volume 4 , November 1938.
• Albrecht, F.: Theoretical investigation of accretion of aerosol particles in an air, stream and an application of the theory of the aerosol filter. Phys. Z 32 (1931): 48-56.
• Langmuir, Irving: OSRD report on Screening Smokes No. 490, Dated October 5, 1942 apps.dtic.mil
• Houghton, H. G., and Radford, W. H.: On the Measurement of Drop Size and Liquid Water Content in Fogs and Clouds. Papers in Phys. Oceanography and Meteorol., M.I.T. and Woods Hole Oceanographic Inst., vol. VI, no. 4, Nov. 1938.
• Humphreys, W. J.: Physics of the Air. J. B. Lippincott Co., 1920.
• Kantrowitz, Arthur: Aerodynamic Heating and the Deflection of Drops by an Obstacle in an Air Stream in Relation to Aircraft Icing. NACA-TN-779, 1940.
• Zahm, A. F.: Flow and Drag Formulas for Simple Quadrics, NACA-TR-253, 1927.

An online search ³ found "Super-Cooled Water Droplets in Rising Currents of Cold Saturated Air" cited by 24 publications.

Notes