"this correlation is a first-order approximation of the presently available aerodynamic and icing data for airfoils exposed to icing conditions"

SAE Preprint No. 225, "Correlation of Airfoil Ice Formations and Their Aerodynamic Effects With Impingement and Flight Conditions"

and

NASA-TM-D-2166, "Prediction of Aerodynamic Penalties Caused by Ice Formations on Various Airfoils"

The content of these two publications are almost identical. As NASA-TM-D-2166 is the one that was cited the most, and has a more legible copy available online, I will center the review around it.

Summary

A more general correlation of drag due to ice on an airfoil is developed.

Key Points

1. Several airfoils are studied in addition to the NACA 65A004 previously used.
2. A more general correlation of drag due to ice on an airfoil is developed.
3. For lift, "no systematic relation is readily apparent for a thin, sharp-nosed airfoil such as the 65A004 airfoil".

Abstract

An empirical equation is developed by which changes in drag coefficients due to ice formations on an NACA 65A004 airfoil may be calculated from known icing and flight conditions; this equation is then extended to include available data for other airfoils with thickness ratios up to 15 percent. The correlation was obtained primarily by use of ice heights and ice angles measured on the 4-percent-thick airfoil. The final equation, however, does not include the ice measurements, but relates changes in drag coefficients due to ice with the following variables: icing time, airspeed, air temperature, liquid-water content, cloud-droplet-impingement efficiencies, airfoil chord, angles of attack, and leading-edge radius of curvature.

Changes in lift and pitching-moment coefficients due to ice on an NACA 0011 airfoil are also related to the corresponding changes in drag coefficients; additional data on lift and pitching-moment changes due to ice are limited to the 65A004 airfoil, for which complex trends preclude a general relation scope of this report.

Discussion

NASA-TM-D-2166 was published (in 1964) after the end of the NACA-era. However, it is listed in the "Selected Bibilography of NACA-NASA Aircraft Icing Publications".

A footnote in NASA-TM-D-2166 explains the republication of the data from SAE Preprint 225:

The material contained herein was presented as a paper at the SAE National Aeronautic Meeting, Los Angeles, California, October 4, 1957, under the title "Correlation of Airfoil Ice Formations and Their Aerodynamic Effects with Impingement and Flight Conditions." It is now being published because of present interest in icing protection for light aircraft (CAR-3) and helicopters.

Readers may also note some material reused from NACA-TN-4151 and NACA-TN-4155, which were reviewed previously, and that material will not be repeated here.

A review of the aerodynamic data from these previous icing studies showed that, to understand the effects of ice on airfoil characteristics, it would be necessary to study the exact ice shapes and sizes and to relate the aerodynamic effect of the ice to the known effects produced by surface roughness, flow spoilers, leading-edge flaps, etc., which ice simulates. Such a study was accomplished with icing data for the NACA 65A004 airfoil section shown in figure 1 (ref. 5). In this study, a variety of ice shapes was accurately measured and related to the generating impingement and icing conditions. The changes in airfoil drag coefficients due to ice were then correlated with the ice shapes and, finally, with impingement and flight conditions. The object of this report is to describe this analysis of icing data for the 4-percent-thick airfoil and to extend it to include all the airfoil sections for which aerodynamic data in NACA icing tunnel conditions are available.

PREDICTION OF DRAG CHANGES DUE TO ICE ON VARIOUS AIRFOILS
Because equation (1) for approximating the drag-coefficient changes due to ice on an NACA 65A004 airfoil was determined, it was desirable to attempt a similar relation for other airfoils, although ice measurements were available only for the 4-percent-thick airfoil. Accordingly, all the applicable NACA icing drag data from references 2 to 4 were inserted into equation (1) for trial, and impingement parameters were interpolated from data of reference 6. These icing data are listed in table I. It was found that an airfoil thickness trend appeared; to account for this trend, a factor r was introduced, which is the airfoil leading-edge radius of curvature in percent of chord. Also, in the absence of more knowledge as to the effect of sweep on drag due to ice formations, the 63A009 airfoil (sweep angle, 36°) was regarded for correlation purposes as an unswept two-dimensional airfoil, except that impingement, chord length, and radius of curvature were taken for the stream wise cross section of the airfoil.

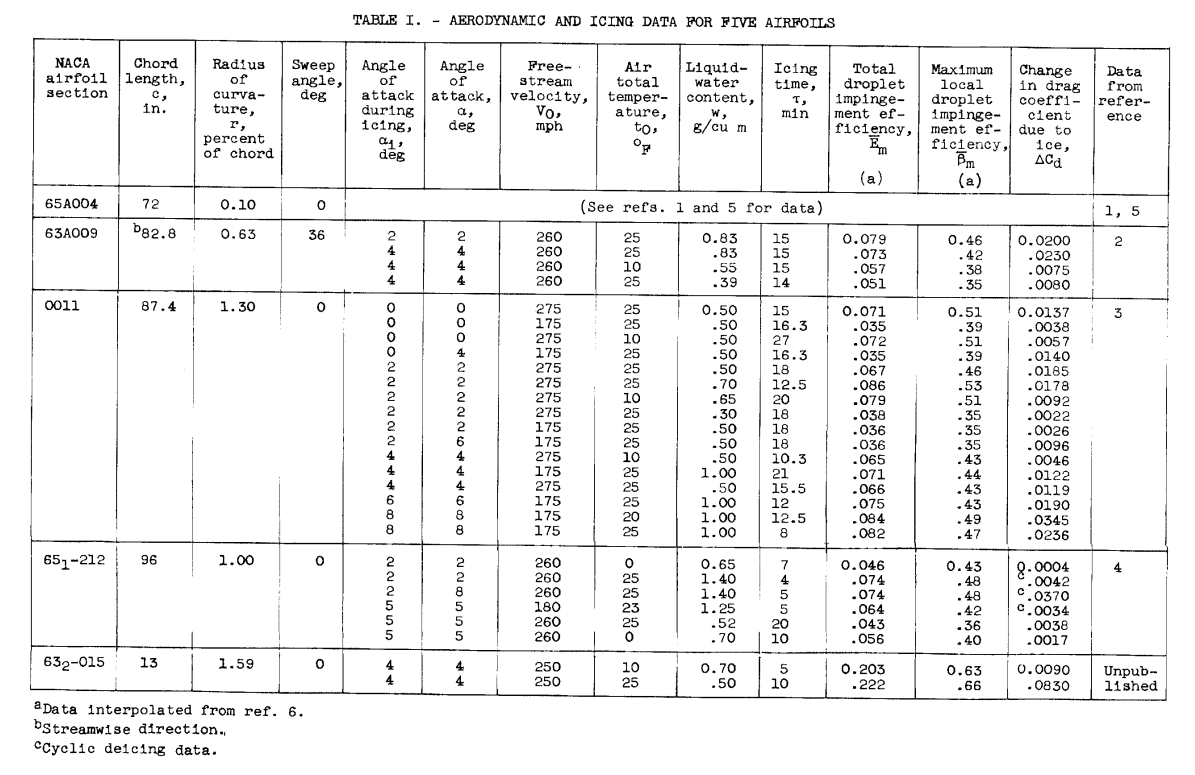
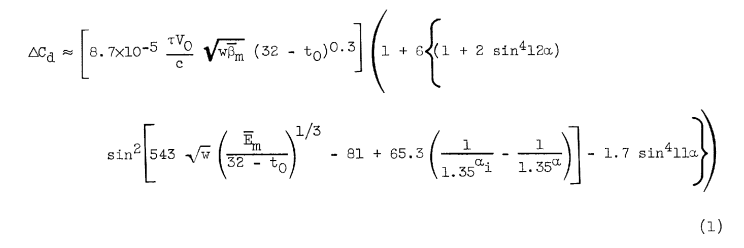
A final equation was derived that represents the available icing drag data of the referenced airfoils and that is consistent with equation (1) for the 4-percent-thick airfoil:

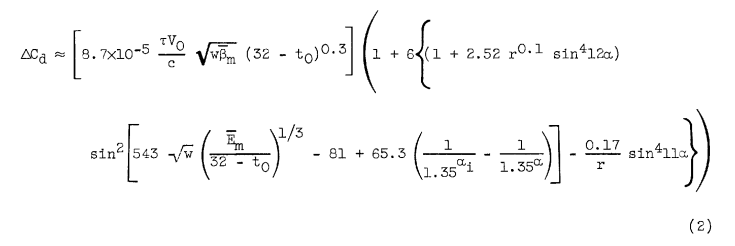
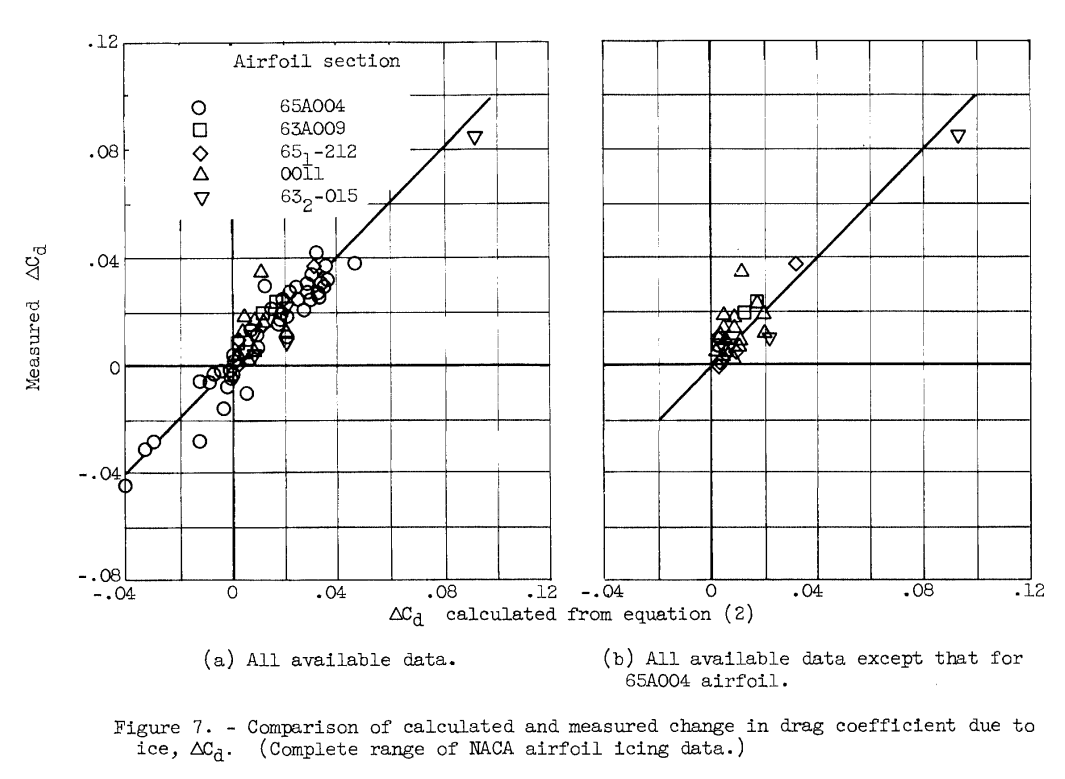
Measured values of ΔCd from table I and reference 5 are plotted in figure 7 against the values calculated by using equation (2). The order of agreement shown in figure 7 appears quite satisfactory, considering the nature and difficulty of obtaining aerodynamic, impingement, and meteorological data in icing conditions.

Unfortunately, changes in lift and pitching-moment coefficients due to ice formations are known only for NACA0011 (ref. 3) and 65A004 (ref. i) airfoils. In addition to these data, however, it should be possible to estimate changes in lift and moment coefficients by utilizing relations in the published aerodynamic characteristics of airfoils with and without flaps, spoilers, protuberances, etc.

From the limited data available in icing conditions, it appears that changes in lift and moment coefficients due to ice formations can be related to the concurrent changes in drag coefficients for a thick, blunt airfoil such as the 0011 airfoil, whereas no systematic relation is readily apparent for a thin, sharp-nosed airfoil such as the 65A004 airfoil. The relations between changes in lift, moment, and drag coefficients due to ice on the 0011 airfoil are shown in figure 8 as functions of geometric angle of attack (data of ref. 3). Well-established trends are evident in figure 8, wherein increases in drag coefficients are accompanied by similar increases in moment coefficients and by decreases in lift coefficients of generally larger magnitude. These trends are similar to the trends with the 65A004 airfoil, but only up to angles of attack of about 3°. At higher angles of attack, changes in lift and moment coefficients due to ice on the 4-percent-thick airfoil were erratic with respect to changes in drag coefficients, primarily because of the flow separation from the upper surface starting at an angle of attack of about 4° (ref. 1).

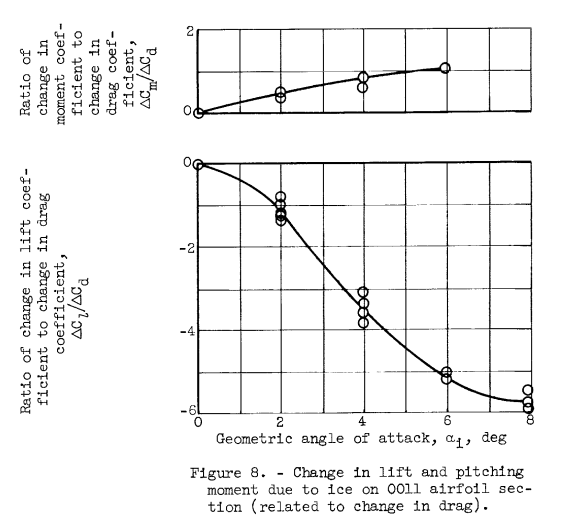
Conclusions

It should be noted in conclusion that this correlation is a first-order approximation of the presently available aerodynamic and icing data for airfoils exposed to icing conditions in the NACA icing tunnel. Several factors that were thought to be secondary in importance were ignored in this analysis. The correlation should be useful, however, in estimating the type and size of ice formations that would result from any specified icing encounter, in estimating the aerodynamic penalties that would result from an encounter, and in making flight performance studies in which icing effects must be evaluated.

See "Related" below for a later comparison of icing wind tunnel test data to NASA-TM-D-2166 calculations, illustrating the limitations of "a first-order approximation".

Citations

SAE Preprint 225 and NASA-TM-D-2166 both cite the same 6 publications:

• Gray, Vernon H., and von Glahn, Uwe H.: Aerodynamic Effects Caused by Icing of an Unswept NACA 65A004 Airfoil. NACA-TN-4155, 1957.
• von Glahn, Uwe H., and Gray, Vernon H.: Effect of Ice Formations on Section Drag of Swept NACA 63A-009 Airfoil with Partial-Span Leading-Edge Slat for Various Modes of Thermal Ice Protection. NACA-RM-E53J30, 1954.
• Bowden, Dean T.: Effect of Pneumatic De-Icers and Ice Formations on Aerodynamic Characteristics of an Airfoil. NACA-TN-3564, 1956.
• Gray, Vernon H., and von Glahn, Uwe H.: Effect of Ice and Frost Formations on Drag of NACA 651_212 Airfoil for Various Modes of Thermal Ice Protection. NACA-TN-2962, 1953.
• Gray, Vernon H.: Correlations Among Ice Measurements, Impingement Rates, Icing Conditions and Drag Coefficients for an Unswept NACA 65A004 Airfoil. NACA-TN-4151, 1958.
• Gelder, Thomas F., Smyers, William H., Jr., and von Glahn, Uwe H.: Experimental Droplet Impingement on Several Two-Dimensional Airfoils with Thickness Ratios of 6 to 16 Percent. NACA-TN-3839, 1956.

An online search found NASA-TM-D-2166 cited 47 times ³. No citations for SAE Preprint 225 were found.

Related

NASA-TM-83556 ⁴ compares measured ice drag on a NACA0012 airfoil to NASA-TM-D-2166 ("ref. 1") calculations. Several of the calculated delta Cd values are notably higher than the test values.

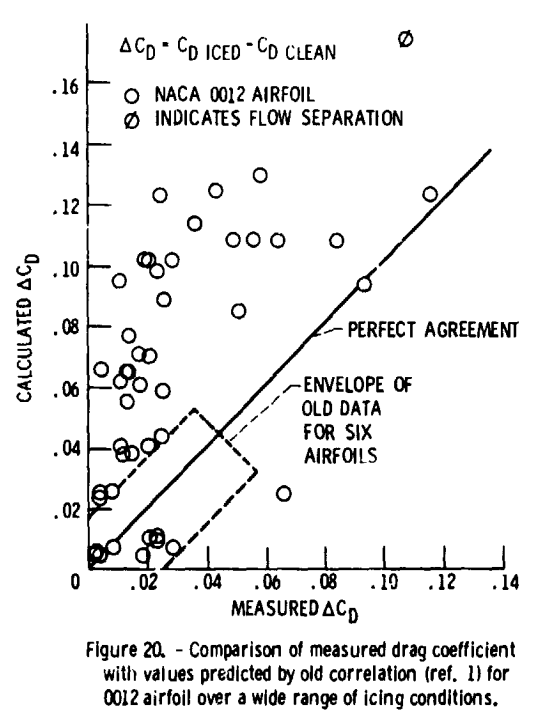
Data for the NACA0012 airfoil was not included in the NASA-TM-D-2166 data, but the similar NACA0011 airfoil was included.

We will see more from NASA-TM-83556 in the "Conclusions of the Ice Shapes and Their Effects Thread", and in the upcoming "Icing Wind Tunnel Test Thread".

Notes: