"radome icing has serious effects on the radar operation"

"An Analytical Study of Heat Requirements for Icing Protection of Radomes"

Abstract

The heat requirements for the icing protection of two radome configurations have been studied. over a range of design icing conditions. Both the protection limits of a typical thermal protection system and the relative effects of the various icing variables have been determined. For full evaporation of all impinging water, an effective heat density of 14 watts per square inch was required. When a combination of the full evaporation and running-wet surface systems was employed, a heat requirement of 5 watts per square inch provided protection at severe icing and operating conditions.

Discussion

INTRODUCTION

Radar is becoming of increasing importance in the design and operation of aircraft. Successful operation of these aircraft demands that the performance of the radar system including the radome be unimpaired by environmental factors including icing conditions. Recent experimental investigations have shown that radomes mounted in the nose of an aircraft are very susceptible to icing and that this radome icing has serious effects on the radar operation resulting from a marked decrease in the transmission efficiency and a deflection of the radar beam. Protection of the radome against icing, therefore, is required. This protection can be achieved, in several ways, including: applying a temperature-depressant material to the radome surface, or heating the radome surface sufficiently to prevent the formation of ice. This report will consider only the thermal protection method.

The determination of the heating requirements and the performance of a thermal icing protection system requires many complex calculations. Much of the basic information required. for such a calculation, particularly for a body such as a radome operating at high speeds, is not always readily available nor in a form directly applicable for engineering design purposes. For these reasons, the performance of a radome thermal icing protection system has been studied at assumed operational and icing conditions. The objectives of this study, which was conducted at the NACA Lewis laboratory, were to determine the protection requirements for a typical thermal icing protection system and to study the relative effects of the various icing variables on these protection requirements.

ANALYSIS

This investigation is divided into two parts: (1) a study of protection requirements for complete evaporation of all the water impinging upon the radome, resulting in a dry surface, and (2) a study of protection requirements for the case of a running-wet condition, that is, only sufficient heat is supplied, to maintain the coldest point on the surface of the radome at 32° F and thus prevent the formation of ice on the radome. In this latter method, the excess water not evaporated from the radome surface will flow aft and freeze on the unheated. portions of the aircraft.

Evaporation of Impinging Water

For the case of complete evaporation of all the impinging water, the heat- and mass-transfer relations given in references 1 and 2 may be written in the following form

hav (ts-to) + 2.82 L hav K (es/p1 - e0/p0) + cw mav (ts-t)   
= (hav Vo^2)/(2 g J cp) (1-(V1/V0)^2 (1+r) + mav V0^2 / (2 g J) + q   (1)

References 1 and 2 are:

• Gelder, Thomas F., Lewis, James P., and Koutz, Stanley L.: Icing Protection for a Turbojet Transport Airplane: Heating Requirements, Methods of Protection, and Performance Penalties. NACA-TN-2866, 1953.
  > review: Compressed air heat
• Gray, Vernon H.: Simple Graphical Solution of Heat Transfer and Evaporation from Surface Heated to Prevent Icing. NACA-TN-2799, 1952 ntrs.nasa.gov.
  > review: NACA-TN-2799

All symbols are defined in appendix A. In order to simplify the calculations, average values are used in this equation rather than calculations made at local points all over the radome surface and integration of these results. In addition, the heat quantities are the heat requirements at the radome surface and do not represent the heat-source requirement.

The heat required for evaporation is

qc = mav L   (2)

The heat available for evaporation is

qe = 2.82 hav L (es/p1 - e0/p0)   (3)

For complete evaporation equation (2) must equal equation (3), or

2.82 (es/p1 - e0/p0) = mav / hav   (4)

The average, rate of water impingement is given by

mav = 0.3296 Em V0 Ap / As w     (5)

The collection efficiency Em is defined as the ratio of the amount of water actually impinging upon a body to the amount of cloud water which would be swept out by the area of the body projected in the flight direction. This collection efficiency is a function of body size and shape, airspeed, temperature, pressure, and water droplet size. The values of collection efficiency used in this analysis were obtained from the data of reference 3 and unpublished experimental data.

Reference 3 is

• Langmuir, Irving, and Blodgett, Katherine B.: A Mathematical Investigation of Water Droplet Trajectories. Tech. Rep. No. 5418, Air Materiel Command, AAF, Feb. 19, 1946. (Contract No. W-33-038-ac-9151 with General Electric Co.)
  books.google.com
  > review: Mathematical Investigation of Water Droplet Trajectories

Reference 3 has impingement data for a sphere, but not a radome. Perhaps a sphere with the leading edge radius of curvature was used as an estimate.

Unfortunately, the "unpublished experimental data" is not further detailed.

The latent heat of vaporization L was taken as 1060 Btu per pound, K as 1.0, V1 as 0.87*V0, and r as 0.85. Assuming values of to and corresponding values of Pa and Em for a given condition of airspeed and effective heat input q, equations (1), (4), and (5) were solved simultaneously by trial and error for the limiting values of liquid-water content. This value of liquid-water content represents the maximum value for the assumed conditions for which all the impinging water will be evaporated within the heated surface area of the radome. An airspeed of 600 miles per hour was assumed throughout the study together with an effective heat density of 2100 Btu per hour per square foot, equal to 4 watts per square inch. This heat density was considered to be uniform over the surface area of the radome.

Icing Conditions

The degree of protection afforded a vulnerable aircraft component by a thermal icing protection system is dependent upon the icing conditions that will be encountered as well as upon the availability of heat and the system efficiency. Thus, in the design and in the appraisal of a protection system, the expected. icing conditions must be studied and established in order to obtain answers that are of reasonable engineering validity. The important variables that must be considered in defining an icing condition are the cloud liquid-water content, the water droplet size and size distribution, the air temperature and pressure, and the extent and frequency of occurrence of a particular type of cloud. Extensive studies of these factors and their combinations have been made by the NACA. Statistical studies of icing conditions and methods of determining the proper combination of the important icing variables have been reported in references 4 and 5.

References 4 and 5 are

• Hacker, Paul T., and Dorsch, Robert G.: A Summary of Meteorological Conditions Associated with Aircraft Icing and a Proposed Method of Selecting Design Criterions for Ice-Protection Equipment. NACA-TN-2569, 1951.
  > review: NACA-TN-2569
• Lewis, William, and Bergrun, Norman R.: A Probability Analysis of the Meteorological Factors Conducive to Aircraft Icing in the United States. NACA-TN-2738, 1952.
  > review: NACA-TN-2738

In the selection of the variables defining an icing condition, the collection efficiency of the body must also be considered since it is as important as the cloud water content and cloud extent in determining the severity of a particular icing condition. The collection efficiency of the radomes considered in this analysis was used (as indicated in ref. 4) to determine the particular combination of values of liquid-water content and droplet size for a particular frequency of occurrence that resulted in the maximum rate of impingement.

Since the heat requirements for a thermal protection system are dependent on the air temperature, it was decided to employ a temperature-altitude relation representative of icing conditions. Reference 4 presents the observed variation of air temperature and pressure altitude in icing conditions. Considerable variation in air temperature for a given altitude is shown by these data; and for this reason and also to obtain a more realistic basis for appraisal of the protection system, the temperature-altitude curves shown in figure 1 were selected.

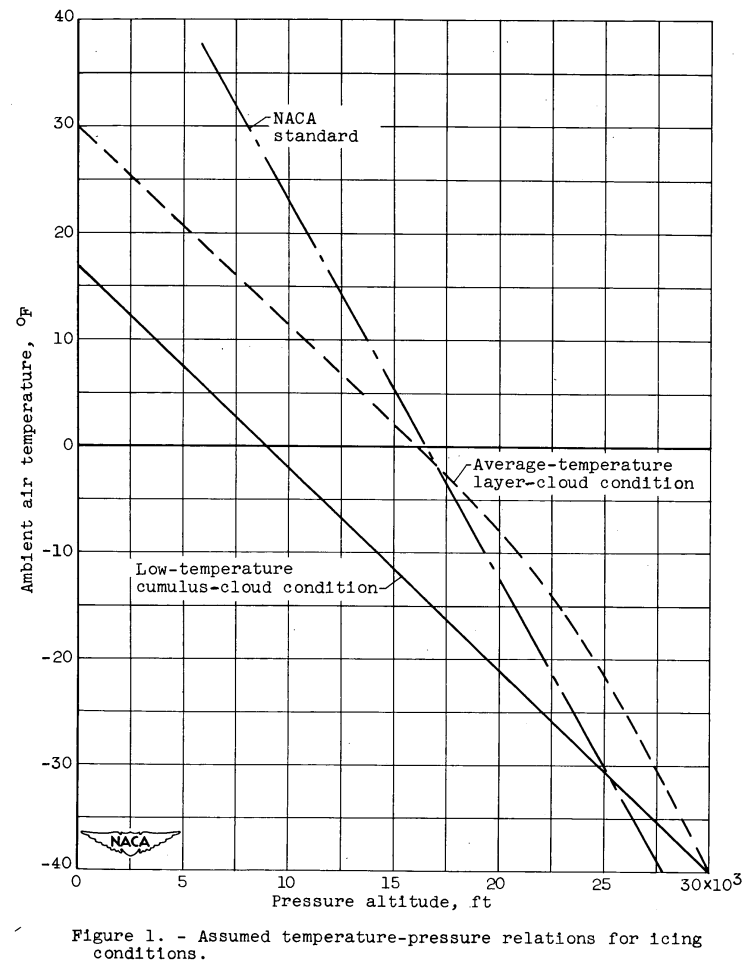
One curve represents the average of the data of reference 4, while the second curve is a fairing through the points of lowest temperature reported in reference 4. The NACA standard atmosphere is also given in figure 1 for comparative purposes. From these temperature-altitude relations and from an assumed exceedence probability of 1 in 1000, the particular combinations of liquid-water content and droplet size which gave maximum rate of impingement were chosen from the curves of reference 5.

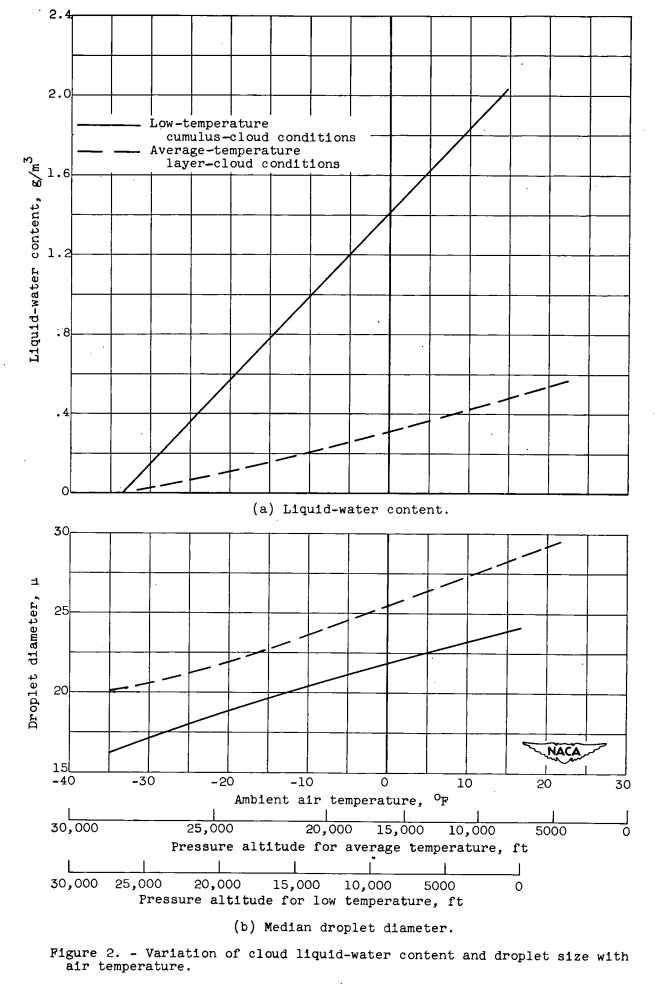
The liquid-water content and droplet size corresponding to cumulus clouds were taken for the low-temperature condition as representing extremely severe icing conditions, while layer cloud values were taken for the average temperature conditions as being typical of average icing conditions, especially with respect to extent of the condition and as the limit for which the full evaporation system would. provide protection. The resultant curves of liquid-water content and droplet size against air temperature are shown in figure 2. The droplet size distribution assumed in the analysis is shown in figure 3.

The basis of the assumptions for Figure 3 are not explained. However, the distribution is vaguely like a Langmuir D or E distribution.

Miscellaneous Assumptions

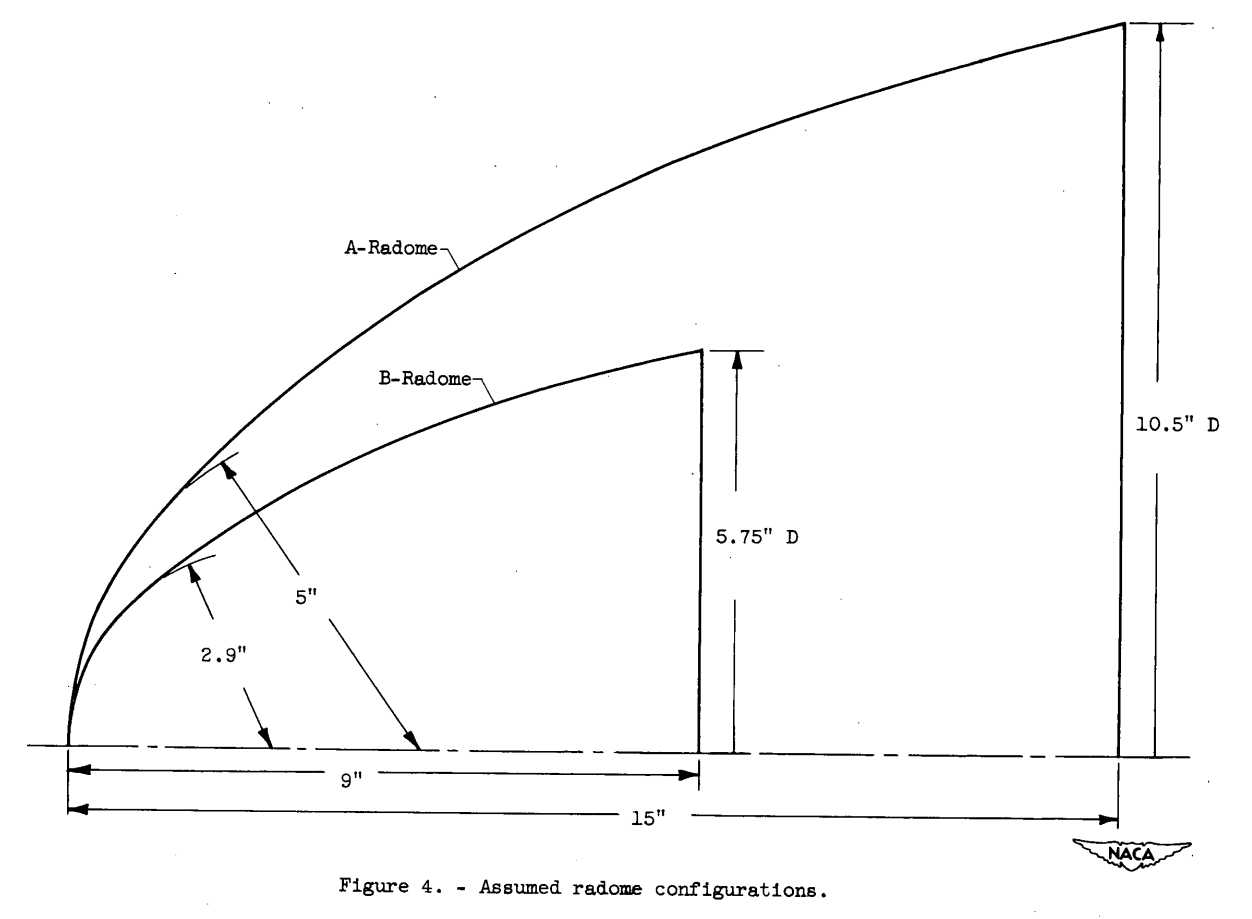
In addition to the icing conditions, several other factors were assumed for the purposes of the analysis. Two radome configurations were investigated, half-sections of which are shown in figure 4, together with the pertinent dimensions. Both radomes, which were assumed to be nose installations, were portions of ellipsoidal bodies of revolution. It was assumed that protection was required to the rear of the radomes.

The convective heat-transfer coefficient was calculated from unpublished experimental data obtained from tests of similar bodies in the icing research tunnel.

The heat transfer data is perhaps in NACA-EM-E53F02, which cites NACA-RM-E53A22 and was published later in the year 1953.

• von Glahn, Uwe H.: Preliminary Results of Heat Transfer from a Stationary and Rotating Ellipsoidal Spinner. NACA-EM-E53F02, 1953.

RESULTS AND DISCUSSION

The results of this analysis are presented for the two radome configurations for the assumed icing conditions.

A-Radome

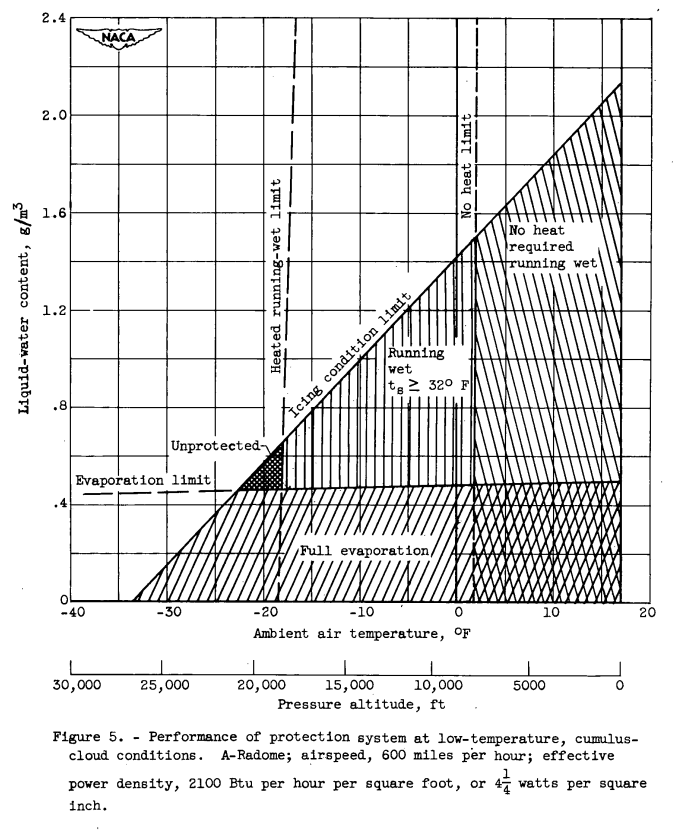
Low-temperature, cumulus condition. - The performance of the protection system for the blunt A-radome at the low-temperature cumulus-cloud condition is shown in figure 5.

The assumed icing conditions taken from figure 2 are designated as the icing limit, and it is assumed that no protection is necessary for conditions to the left of this curve. For the case in which no heat is applied ter the radome, an ice-free running-wet surface for certain conditions results from the kinetic temperature rise. This condition is obtained for all temperatures above approximately 2° F (equivalent to approximately 8000 ft). With the assumed heat density of 41 watts per square inch, the limit for the ice-free running-wet condition becomes approximately -18° F. For all air temperatures to the right of this curve and for the values of liquid-water content shown, the surface temperature will be equal to or greater than 32° F with varying percentages of the impinging water being evaporated. As indicated by both the heated and unheated running-wet curves, the requirement for this condition is almost independent of variations in liquid-water content and is almost entirely dependent upon the air temperature.

For the case of full evaporation, in which the radome surface is maintained dry, the limiting liquid-water content varies from approximately 0.45 gram per cubic meter at -30° F to 0.5 gram per cubic meter at 20° F. The surface will be kept dry for all liquid-water and air-temperature conditions below the full evaporation curve. For the case of full evaporation, the calculated average surface temperature varied, from approximately 63° to 76° F. In contrast to the case of the running-wet condition, the requirement for full evaporation is almost independent of variations in air temperature.

The area below the icing-condition-limit curve that is not protected either by full evaporation or the running-wet condition is seen to be rather small. In this region, ice resulting from both direct water impingement and from runback and refreezing on the radome surface will be obtained.

In order to obtain an estimate of the heat density required for protection over the full range of expected icing conditions, calculations were made of the variation of the heat requirement with water content and with air temperature for the full evaporation and running-wet systems, respectively, at specific values of altitude, droplet size, temperature, and liquid-water content. These results are presented in figures 6 and 7 for the A-radome. The effect of kinetic heating is indicated in figure 6 by the evaporation of water up to 0.09 gram per cubic meter without the application of heat. The heat requirement for full evaporation is seen to vary almost linearly with liquid-water content; the heat requirement for a running-wet surface also approaches a linear relation with air temperature. From an extrapolation of the relations of figure 6, it is determined that protection by means of full evaporation alone over the full range of icing conditions would require an effective heat density of approximately 14 watts per square inch. Full protection by a combination of the evaporation and running-wet surface systems over the entire range of expected icing conditions could. be achieved, with an effective heat density of approximately 5 watts per square inch.

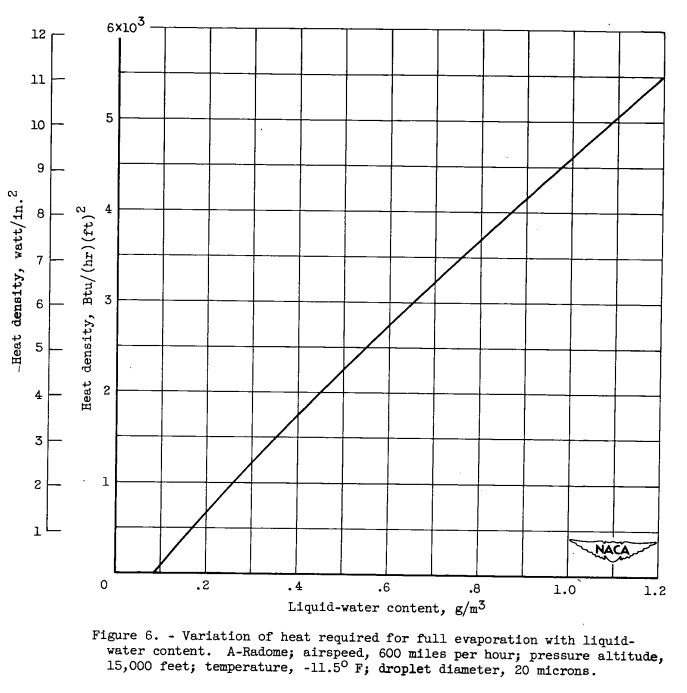
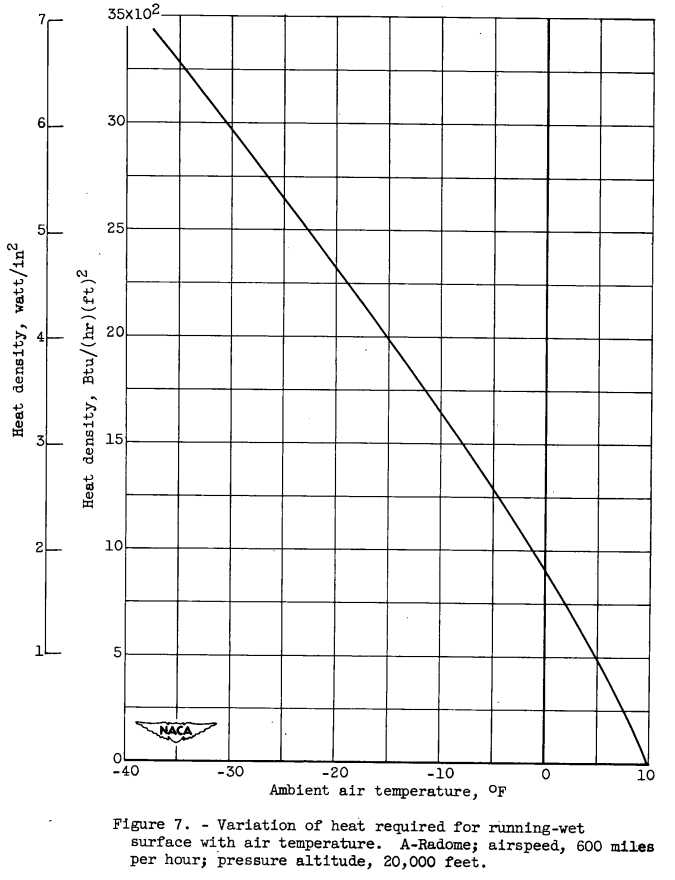
For brevity, the results for the average-temperature condition is not detailed herein.

Only results for the A-Radome are discussed herein.

Conclusions

CONCLUDING REMARKS

In the analysis presented herein it was necessary to make several assumptions. It is believed, that most of these assumptions, including the icing conditions, are of reasonable validity. The most important assumptions that might be questioned are the impingement efficiency and the assumption of an average or uniform effective heat density. The impingement efficiencies used in the analysis are based upon the values for spheres given in reference 3 and upon experimental results for similar radomes obtained at lower airspeeds. For the case of the running-wet surface, the value of the assumed local impingement efficiency is relatively unimportant since, as shown by the results of the analysis, the heat requirement is almost independent of the amount of water caught. For the case of full evaporation the heat requirement, as indicated by the results of figure 6, is directly dependent on the amount of water caught. The total collection efficiencies are regarded as accurate within at least ±10 percent. Based upon the results of figure 6, the heat requirements in the range of interest have approximately the same degree of accuracy.

A more important limitation of the results for the case of full evaporation is the fact that a uniform heat density over the radome surface was assumed and the calculations were made on an average basis rather than by computing the system performance on a point-to-point basis from the radome nose aft. The attainment of both a uniform heat density and surface temperature is impossible and, practically, even the attainment of uniform heat density would be extremely difficult. It is believed, however, that the use of average values in the calculation of the performance of the protection system is valid for the purposes of this analysis as indicating within the limits of engineering accuracy the order of magnitude of the limits of performance of the protection system and the variation of these limits with the important icing variables.

The results of the analysis have indicated that Icing protection of a radome by a thermal protection system can be achieved with reasonable values of heat density even at extreme combinations of operating and icing conditions. For full evaporation of all impinging water, an effective heat density of 14 watts per square inch is required. By employing a running-wet surface system over part of the temperature range and full evaporation over the remainder, protection over the full range of icing conditions can be achieved with an effective heat density of 5 watts per square inch. The heat requirement for full evaporation is dependent primarily upon the rate of water catch or, in terms of the icing condition, the cloud liquid-water content. For the running-wet surface condition, the heat requirement is primarily a function of the ambient air temperature. The use of the running-wet surface system will be dependent not only on the effects of a water film on radar operation but also on the tolerance of the aircraft for runback ice formations aft of the radome.

The "serious effects" mentioned in the introduction of radome ice on the performance of radar depend on the specific radar being used and the performance requirements. Many commercial airplanes with weather radar do not have radome ice protection.

Citations

This publication is cited five times, per scholar.google.com.

Notes