"square orifices ... provided that a jet dimension equal to the diameter of the equivalent area circle was used"

"Investigation of Flow Coefficient of Circular, Square, and Elliptical Orifices at High Pressure Ratios" ¹

Abstract

An experimental investigation was conducted to determine the penetration of air jets directed perpendicularly to an air stream. Jets issuing from circular, square, and elliptical orifices were investigated and the jet penetration at a position downstream of the orifice was determined as a function of jet density, jet velocity, air-stream density, air-stream velocity, effective jet diameter, and orifice flow coefficient. The jet penetrations were determined for nearly constant values of air-stream density at three tunnel-air velocities and for a large range of jet velocities and densities. The results were correlated in terms of dimensionless parameters and the penetrations of the various shapes were compared.

Greater penetration was obtained with the square orifices and the elliptical orifices having an axis ratio of 4:1 at low tunnel air velocities and low jet pressures than for the other orifices investigated. The square orifices gave the best penetrations at the higher values of tunnel-air velocity and jet total pressure.

Discussion

INTRODUCTION

A circular jet directed perpendicularly to an air stream can be satisfactorily utilized as a means of heating or cooling an air stream (reference 1). A later investigation (reference 2) showed that square and elliptical orifices give higher flow coefficients than circular orifices. Better penetrations might therefore be obtained with orifice shapes·other than circles. In addition, a large variation of flow coefficient with jet-pressure ratio was observed in the investigation reported in reference 2. It is possible that better correlation of the data of reference 1 could be obtained by including the flow coefficient in the analysis of the data presented therein.

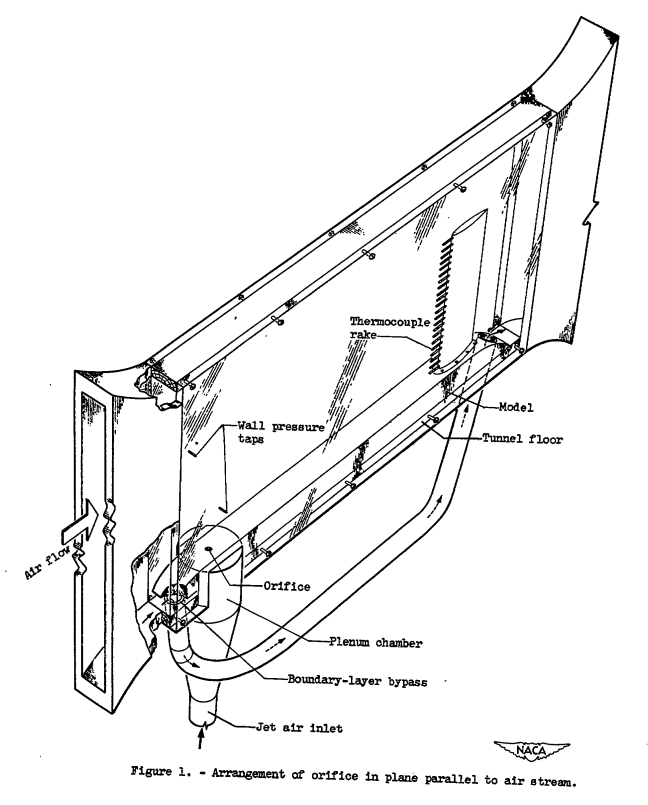
An investigation to determine the penetration of air jets issuing from circular, square, and elliptical orifices was undertaken in a 2- by 20-inch-duct tunnel at the NACA Lewis laboratory, and a study of the effect of variation in the orifice flow coefficient on the correlation of the experimental data was made. The jet penetration at a fixed position downstream of the orifices was determined at tunnel-air velocities of 160, 275, and 380 feet per second for circular, square, and elliptical orifices. Each orifice was investigated over a range of pressure ratios from 1.15 to 3.2 and at a jet total temperature of approximately 400° F.

RESULTS AND DISCUSSION

The analysis of reference 1 indicates that the penetration coefficient l/Dj can be correlated in terms of the jet Reynolds number ρj Vj Dj / μj, the velocity ratio Vj/Vo, the density ratio ρj/ρ0, the viscosity ratio µj/µ0, the mixing distance-diameter ratio s/Dj, and the width_coefficient w/Dj. Depth of penetration defined in reference 1 as the point at which the temperature is 1 F above the free-stream total temperature, wao obtained from the temperature profiles measured at the thermocouple rake.

The primary factors in the correlation of the penetration data are density ratio, velocity ratio, and mixing distance-diameter ratio, as indicated by the results of reference 1. The effect of the other parameters was not evident because no consistent trends could be observed in the data. Appreciable over-all scatter of the data, however, indicated that not all the necessary variables were included in the analysis. The analysis of reference 1 does not include an effect of jet Mach number, that is, pressure ratio. The scatter evident in reference 1 may be caused in part by the variation of flow coefficient with pressure ratio shown in reference 2. In addition to the effect of jet Mach number on the flow coefficient noted in reference 2, a small effect of jet Reynolds number on the flow coefficient was observed as well as a small effect of width coefficient on the jet flow.

The inclusion of the flow coefficient in the analysis might eliminate mch of the data scatter already discussed by including in part some effect of jet Mach number, jet Reynolds number, and width coefficient. Because the flow coefficient is the ratio of the actual flow to the theoretical flow, it may also be considered as a ratio of the effective jet area to the geometric orifice area. The effective jet diameter is therefore related to the geometric diameter by the square root of the flow coefficient.

In order to investigate the effect of flow coefficient on the data correlation, a plot similar to that in reference 1 was made of the penetration coefficient as a function of the product of the density ratio, the velocity ratio, and the square root of the mixing distance-diameter ratio (fig. 2).

The flow coefficients were then calculated by the methods presented in reference 2 and the data in figure 2 were replotted (fig. 3), with the effective jet diameter C^0.5 Dj replacing the actual jet diameter Dj in the parameters. A comparison of figures 2 and 3 indicates that the scatter bas been reduced by using the flow coefficient in the correlation. It is therefore evident that the correlation is improved when the actual jet diameter is replaced by the effective jet diameter. Hereinafter the penetration coefficient and mixing distance - diameter ratio are based on the effective jet diameter and are redefined as l / C^0.5 Dj, and s/ C^0.5 Dj, respectively.

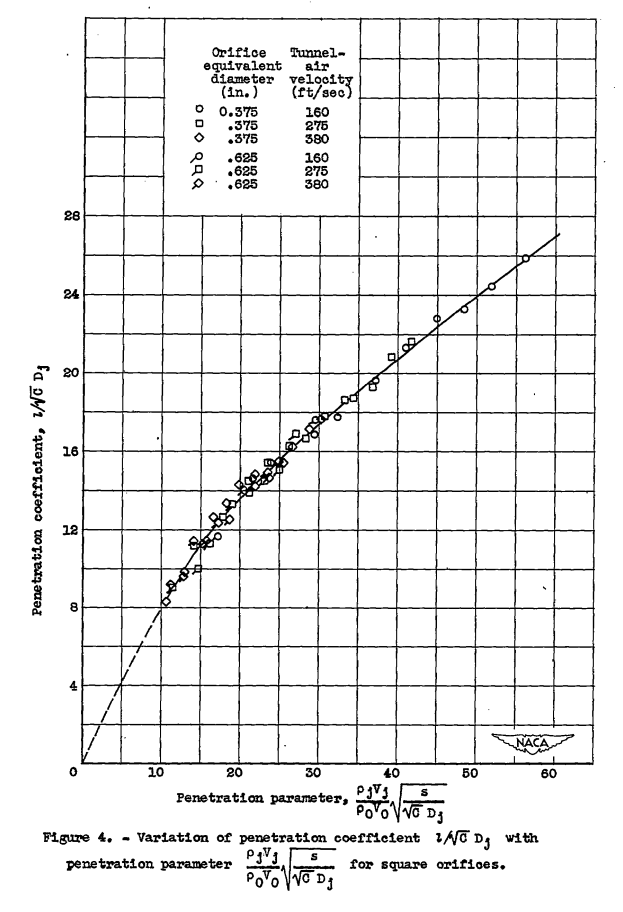
The analysis of the penetrations obtained with the square orifices was conducted in a manner similar to that employed for circular orifices. The penetration coefficient was first plotted as a function of the product of the density ratio and. the velocity ratio. For each square orifice, the penetration coefficient was based on the diameter of the equivalent-area circle and in both cases single-curves were obtained. Because the two curves for the square orifices were similar to those obtained for the circles of the same area, the penetration coefficients for both square orifices were plotted as a function of the product of the density ratio, the velocity ratio, and the square root of the mixing distance - diameter ratio (fig. 4); as for the circular-orifice data, a single curve was obtained. A comparison of figures 3 and 4 shows that slightly higher penetration coefficients were obtained with square orifices than with circular orifices.

A similar procedure was first employed in the correlation of the data obtained with the elliptical orifices. A plot was made of the penetration coefficient as a function of the product of the density ratio and the velocity ratio using a penetration coefficient based on the equivalent-area circle. Results obtained with the ellipse having an axis ratio of 4:1 and an area equivalent to a 0.575-inch-diameter circle are shown in figure 5.

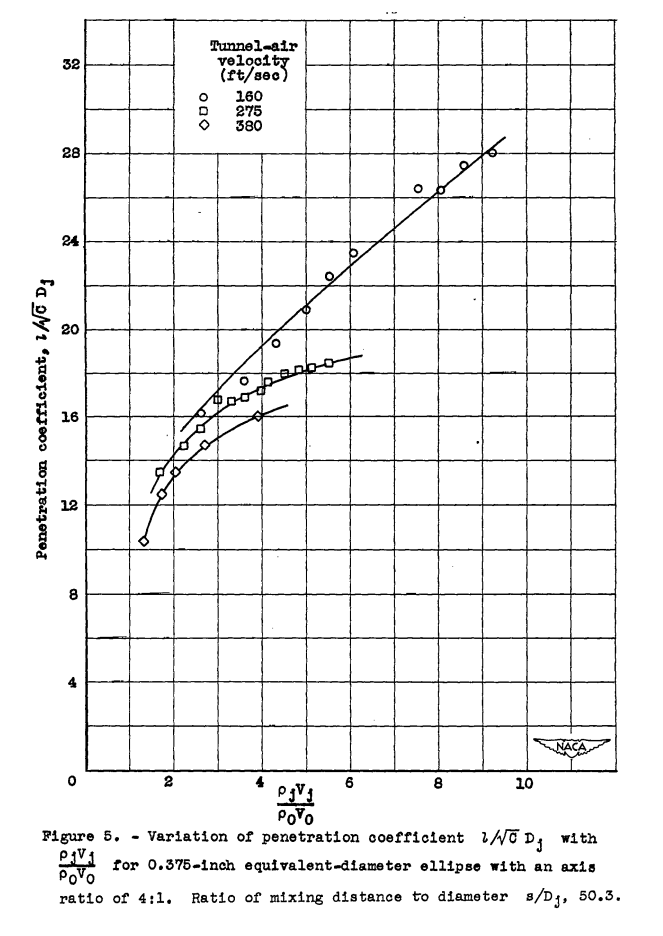
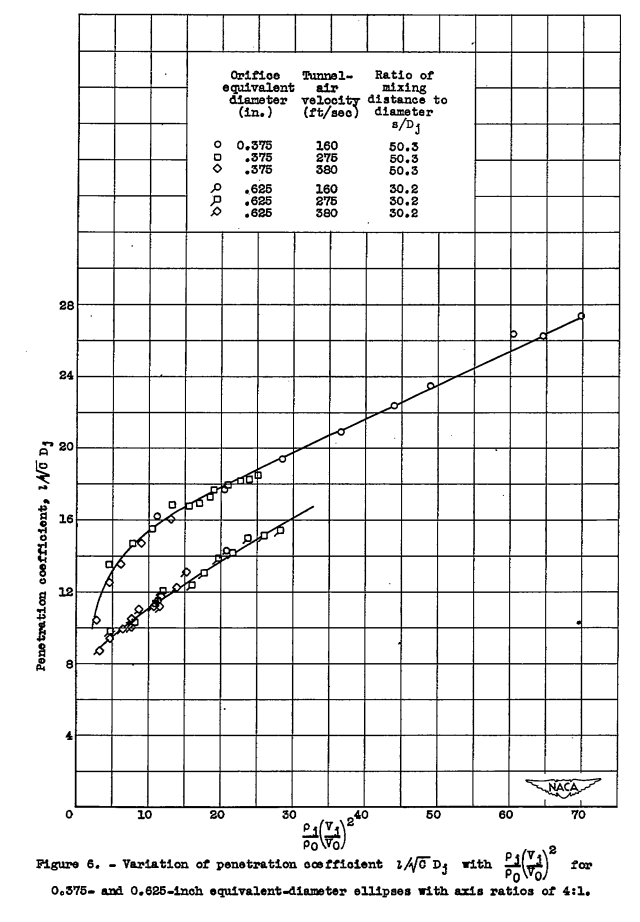
Three separate curves dependent on the tunnel-air velocity were obtained. Further analysis of these data showed that correlation could be obtained provided the penetration coefficient was plotted as a function of the product of tbe density ratio and the square of the velocity ratio, as shown in figure 6. The data for the 0.625-inch equivalent diameter ellipse with an axis ratio of 4:1 were then plotted in terms of the same parameters and again a single curve was obtained (fig. 6). Comparison shows that the curves in figure 6 are separated by a function of the equivalent diameter. Because of the shape of the curves at the lower values of the parameter and because they become approximately parallel at the higher values of the parameter, it is not possible to correlate the data for both ellipses in terms of the ratio of mixing distance to diameter and obtain a single curve. It should be possible, however, to interpolate between the two curves and obtain values at other ratios of mixing distance to diameter s/Dj.

Conclusion

The following results were obtained from an investigation to determine the penetration of air jets issuing from circular, square, and elliptical orifices directed perpendicularly to an air streams
1. The use of the flow coefficient to obtain an effective jet diameter provided better correlation of the penetration coefficients of circular orifices in terms of the usual parameters of density ratio, velocity ratio, and mixing distance-diameter ratio.
2. The penetration coefficient obtained with square orifices could be correlated with the same parameter used for the circles, provided that a jet dimension equal to the diameter of the equivalent area circle was used.
3. It was possible to correlate the ellipse data in terms of the product of the density ratio and the velocity ratio raised to a power. The power to which the velocity ratio must be raised for correlation increased with increasing axis ratio. 4. Greater penetrations were obtained with square orifices than with circular orifices of equal area.
5. At low tunnel airspeeds and low jet pressures greater penetration was obtained with the square orifices and the elliptical orifices having an axis ratio of 4:1 than with the other orifices investigated. The square orifices gave the best penetrations at the higher values of tunnel-air velocity and jet total pressure.

Notes